資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究用 C++ 統計節點權重與 X 相加為斐波那契數的節點數量
給定一棵二叉樹，其節點權重為數字。目標是找到權重為斐波那契數的節點數量。斐波那契數列中的數字為：0、1、1、2、3、5、8、13……第 n 個數是第 (n−1) 個數和第 (n−2) 個數的和。如果權重為 13，則它是一個斐波那契數，因此該節點將被計數。
例如
輸入
temp = 1。輸入值後建立的樹如下所示：
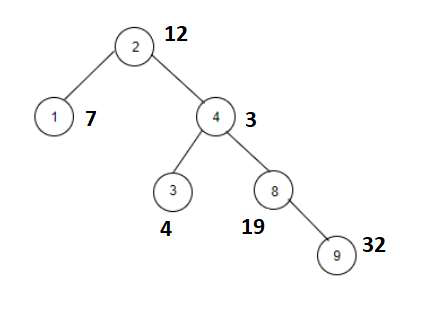
輸出
Count the nodes whose sum with X is a Fibonacci number are: 3
解釋
we are given with the tree nodes and the weights associated with each node. Now we check whether the temp+weight is a Fibonacci number or not.
| 節點 | 權重 | 權重 + temp = 斐波那契數 | 是/否 |
|---|---|---|---|
| 2 | 12 | 12+1=13 | 是 |
| 1 | 7 | 7+1=8 | 是 |
| 4 | 3 | 3+1=4 | 否 |
| 3 | 4 | 4+1=5 | 是 |
| 8 | 19 | 19+1=20 | 否 |
| 9 | 32 | 32+1=33 | 否 |
輸入
temp = 3。輸入值後建立的樹如下所示：
輸出
Count the nodes whose sum with X is a Fibonacci number are: 3
解釋
we are given with the tree nodes and the weights associated with each node. Now we check whether the temp+weight is a Fibonacci number or not.
| 節點 | 權重 | 權重 + temp = 斐波那契數 | 是/否 |
|---|---|---|---|
| 5 | 23 | 23+3=26 | 否 |
| 2 | 125 | 125+3=128 | 否 |
| 6 | 671 | 671+3=674 | 否 |
| 4 | 212 | 212+3=215 | 否 |
| 5 | 7171 | 7171+3=7174 | 否 |
| 3 | 998 | 998+3=1001 | 否 |
下面程式中使用的方案如下：
在此方案中，我們將對樹的圖形應用深度優先搜尋 (DFS) 來遍歷它並檢查節點的權重和 temp 是否加起來為斐波那契數。為此，請使用兩個向量 Node_Weight(100) 和 edge_graph[100]。
用節點的權重初始化 Node_Weight[]。
使用向量 edge_graph 建立樹。
取一個全域性變數 Fibonacci 並將其初始化為 0。取另一個全域性變數 temp。
函式 check_square(long double val) 獲取一個整數，如果 val 是一個完全平方數，則返回 true。
取 val_1 = sqrt(val)
現在，如果 (val_1 − floor(val_1) == 0) 返回 true，則 total 是一個完全平方數，返回 true。
否則返回 false。
函式 check_Fibonacci(int num) 獲取一個數字，如果它是斐波那契數，則返回 true。
用 5*num*num 初始化 fib。
如果 check_square((fib + 4)) || check_square((fib − 4)) 結果為 true，則返回 true。
否則返回 false。
函式 Fibonacci_number(int node, int root) 返回權重與 X 相加為斐波那契數的節點數量。
如果 if(check_Fibonacci(Node_Weight[node] + temp)) 返回 true，則遞增 Fibonacci。
使用 for 迴圈遍歷向量 edge_graph[node] 中的樹。
對向量中的下一個節點呼叫 Fibonacci_number(it, node)。
在所有函式結束時，我們將擁有一個 Fibonacci 作為權重與 temp 相加為斐波那契數的節點數。
示例
#include <bits/stdc++.h>
using namespace std;
vector<int> Node_Weight(100);
vector<int> edge_graph[100];
int Fibonacci = 0, temp;
bool check_square(long double val){
long double val_1 = sqrt(val);
if(val_1 − floor(val_1) == 0){
return true;
}
return false;
}
bool check_Fibonacci(int num){
int fib = 5 * num * num;
if(check_square((fib + 4)) || check_square((fib − 4))){
return true;
}
return false;
}
void Fibonacci_number(int node, int root){
if(check_Fibonacci(Node_Weight[node] + temp)){
Fibonacci++;
}
for (int it : edge_graph[node]){
if(it == root){
continue;
}
Fibonacci_number(it, node);
}
}
int main(){
//weight of the nodes
Node_Weight[2] = 6;
Node_Weight[1] = 4;
Node_Weight[4] = 23;
Node_Weight[3] = 5;
Node_Weight[8] = 161;
Node_Weight[9] = 434;
//create graph edge
edge_graph[2].push_back(1);
edge_graph[2].push_back(4);
edge_graph[4].push_back(3);
edge_graph[4].push_back(8);
edge_graph[8].push_back(9);
temp = 3;
Fibonacci_number(2, 2);
cout<<"Count the nodes whose sum with X is a Fibonacci number are: "<<Fibonacci;
return 0;
}輸出
如果我們執行上述程式碼，它將生成以下輸出：
Count the nodes whose sum with X is a Fibonacci number are: 1
104 次檢視
