資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究使用 C++ 計算將集合劃分成 k 個子集的方法數
給定兩個數字 e 和 p。目標是計算將集合的 e 個元素劃分成 p 個分割槽/子集的方法數。
例如
輸入
e=4 p=2
輸出
Count of number of ways to partition a set into k subsets are: 7
解釋
If elements are: a b c d then ways to divide them into 2 partitions are: (a,b,c)−(d), (a,b)−(c,d), (a,b,c)−(d), (a)−(b,c,d), (a,c)−(b,d), (a,c,d)−(b), (a,b,d)−(c). Total 7 ways.
輸入
e=2 p=2
輸出
Count of number of ways to partition a set into k subsets are: 1
解釋
If elements are: a b then ways to divide them into 2 partitions are: (a)− (b). Total 1 way only.
以下程式中使用的演算法如下 −
在這個方法中，我們將使用動態規劃方法。解決方案中使用的計算始終是遞迴的。如果我們將元素分成 p 個分割槽，則 −
如果 e-1 個元素可以分成 p 個分割槽，方法數為 ways(e-1,p)。那麼我們可以將當前元素放入這 p 個分割槽中的一個，方法數為 p*ways(e-1,p)。
如果 e-1 個元素分成 p-1 個分割槽，方法數為 ways(e-1,p-1)，那麼將 1 個元素放入單獨的 1 個分割槽的方法數為 1*ways(e-1,p-1)。總方法數將為 p*ways(e-1,p)+ways(e-1,p-1)。此方法將變為遞迴 −
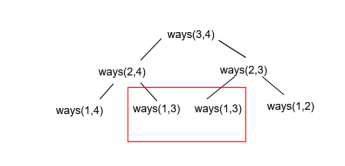
如上所示，將進行重複計算。為了避免這種情況，我們將使用動態規劃方法。
將變數、元素和分割槽作為輸入。
函式 partition_k(int elements, int partition) 獲取這兩個變數並返回將集合劃分成 k 個子集的方法數。
使用二維陣列 arr[elements + 1][partition + 1] 來儲存 ways(e,p) 的值在 arr[e][p] 中。
使用 for 迴圈從 i=0 到 i=elements，設定 arr[i][0] = 0，因為分割槽數為 0，則 ways(i,0)=0。
再次使用 for 迴圈從 j=0 到 i=partitions，設定 arr[0][j] = 0，因為元素數為 0，則 ways(0,i)=0。
現在使用兩個 for 迴圈遍歷 arr[][]，從 i=1 到 i<=elements 和 j=1 到 j<=i，並填充其餘值。
對於單個元素，ways=1，或者對於將 x 個元素分成 x 個分割槽，只有一種方法。因此，如果 i==j 或 j==1，則設定 arr[i][j] = 1。
否則，設定 temp_1 = arr[i-1][j-1] 和 temp_2 = arr[i-1][j]，並更新 arr[i][j] = j * temp_2 + temp_1。
在所有迴圈結束時，我們將有 arr[elements][partition] 作為總方法數。
返回 arr[elements][partition] 作為結果。
示例
#include<iostream>
using namespace std;
int partition_k(int elements, int partition){
int arr[elements + 1][partition + 1];
for(int i = 0; i <= elements; i++){
arr[i][0] = 0;
}
for(int j = 0; j <= partition; j++){
arr[0][partition] = 0;
}
for(int i = 1; i <= elements; i++){
for (int j = 1; j <= i; j++){
if (j == 1 || i == j)
{ arr[i][j] = 1; }
else{
int temp_1 = arr[i−1][j−1];
int temp_2 = arr[i−1][j];
arr[i][j] = j * temp_2 + temp_1;
}
}
}
return arr[elements][partition];
}
int main(){
int elements = 4;
int partition = 2;
cout<<"Count of number of ways to partition a set into k subsets are: "<<partition_k(elements, partition);
return 0;
}輸出
如果我們執行上面的程式碼，它將生成以下輸出：
Count of number of ways to partition a set into k subsets are: 7
465 次瀏覽
