雙極結型電晶體：定義、構造、型別

---

引言

雙極結型電晶體是一種半導體器件。矽或鍺是雙極結型電晶體中使用的兩種半導體材料。兩個P-N結之間形成三層結構，分別稱為發射極、基極和集電極。

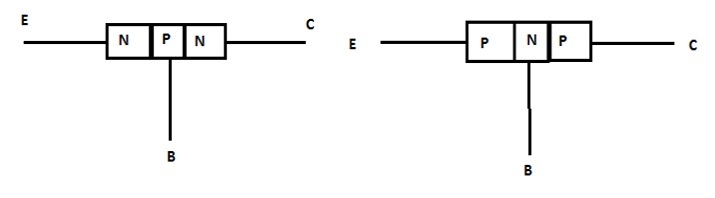
• 發射極層表示為E

• 集電極層表示為C

• 基極層表示為B

電晶體的中間部分稱為基極層（B）。基極層是一層薄層，厚度約為25微米。電晶體的左側層是發射極層（E），右側層是集電極層（C）。

雙極結型電晶體

用於放大訊號的器件，由三層半導體材料和兩個P-N結組成，稱為雙極結型電晶體（BJT）。當施加外部電源時，電晶體即可進行放大。基極層是薄層。電晶體的左側部分是發射極層（E），右側部分是集電極層（C）。發射極層高度摻雜。

但發射極必須提供大多數載流子。基極層與發射極相反，因為它是輕微摻雜的。集電極層也是輕微摻雜的，以接收更多載流子。根據這些特性，我們應該知道集電極和發射極不能互換。

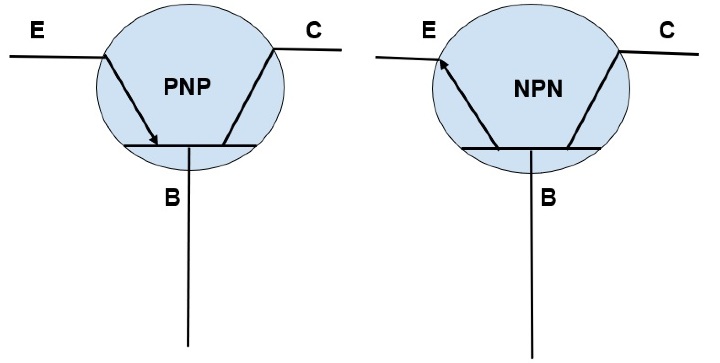
雙極結型電晶體符號

箭頭始終表示電流方向，在每個電晶體中從發射極區域到基極或從基極到發射極（從P到N）。它表示常規電流方向。在PNP電晶體中，箭頭指向基極區域，表示發射極對基極和集電極是正的。在NPN電晶體中，箭頭指向發射極區域，表示基極對發射極是正的。

雙極結型電晶體構造

它由一塊具有兩個連續P-N結的獨立半導體元件構成。矽或鍺是雙極結型電晶體中使用的兩種半導體材料。我們已經知道電晶體由三層組成：發射極、基極和集電極。在PNP電晶體中，有兩個PN接面。左側連線到發射極，中間部分是基極區域，右側是集電極層。E-B和C-B交點是BJT的兩個結。E-B結正向偏置，C-B結反向偏置。

雙極結型電晶體的工作原理

BJT的工作區域包括飽和區、截止區和放大區。

飽和區

拐點的起點稱為飽和區。飽和區位於原點和恆定點之間，在該點集電極電流變得恆定。

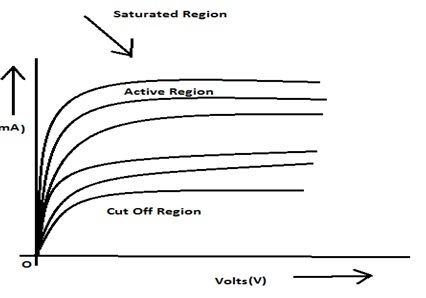
截止區

即使基極電流為零，電晶體中也存在非常低的集電極電流。基極電流為零的低區域稱為截止區。

放大區

放大區位於曲線的中間，位於飽和區和截止區之間。放大區中的拐點是恆定的。在這個區域中，發射極-基極端子正向偏置，集電極-基極端子反向偏置。

雙極結型電晶體的型別

• PNP BJT

• NPN BJT

PNP BJT

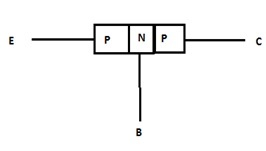
在PNP BJT中，N型材料的兩側都填充有P型半導體。

NPN BJT

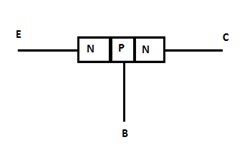
在NPN BJT中，左側和右側填充有N型半導體。P型半導體放置在這兩種半導體之間。當電流進入發射極區域時，它將正號轉換為負號。

雙極結型電晶體的功能

PNP BJT和NPN BJT是兩種型別的雙極結型電晶體。PNP電晶體中存在背靠背的PN接面。由於這兩個結中存在的耗盡層，勢壘增加了。電池提供外部電源。由於正向偏置，大量空穴透過端子進入基極。一些電子從基極進入發射極。這些電子與發射極中的空穴複合。當電子從發射極到基極的漂移增加時，發射極電流I_E增加。同樣，也計算了基極電流和集電極電流。這就是雙極結型電晶體的功能。

雙極結型電晶體的電壓、電荷控制和電流配置

C-E電流控制B-E電流。集電極-發射極電流給出電流-電壓之間的關係。集電極電流中存在集中的次級載流子，因為它具有基極區域。

要操作雙極結型電晶體，有三種類型的電路連線。

• 共基極（CB）模式

• 共發射極（CE）模式

• 共集電極（CC）模式。

BJT的應用

電晶體作為開關

通常BJT用作開關。例如，考慮NPN電晶體的共發射極配置。集電極與負載電阻和基極電阻串聯連線。當輸入為高電平時，電晶體飽和。當電晶體飽和時，電路中將流過最大電流。因此，電晶體處於導通狀態。當輸入為低電平時，基極-發射極結中沒有電流流動。電晶體將處於關斷狀態。

電晶體放大器

放大是雙極結型電晶體的主要功能。

結論

電晶體是一種用於增強訊號的器件，由三層組成。具有兩個P-N結的半導體材料稱為雙極結型電晶體（BJT）。它由三層組成：發射極、集電極和基極。BJT有兩種型別：PNP BJT和NPN BJT。BJT的主要功能是計算三層的電流流動。BJT的應用包括用作開關、放大器、濾波器和振盪器。

常見問題

Q1. 什麼是電晶體偏置？

A1. 當訊號透過電路時，應保持發射極電壓，並選擇合適的執行點。這個過程稱為電晶體偏置。

Q2. 什麼是輸出阻抗？

A2. 在恆定基極電流比下，放大區中C-E電壓變化與集電極電流變化的比值稱為輸出阻抗。

$$\mathrm{輸出阻抗,\:r_0=(\frac{\Delta V_{CE}}{\Delta I_C})I_B}$$

Q3. 電晶體的三個特性是什麼？

A3.

• 輸入特性

• 輸出特性

• 轉移特性

Q4. 請說明電晶體可以工作的偏置條件。

A3.

• 發射極-基極端子正向偏置，以便大量載流子從發射極推回，並且結提供少量電阻。

• 集電極-基極端子反向偏置，以便它接受大量載流子，並且結對電流提供大量電阻。

Q5. 定義電流增益β

A5. 在恆定的集電極-發射極電壓下，集電極電流變化與基極電流變化的比值稱為電流增益。

$$\mathrm{電流增益\:β=(\frac{\Delta I_C}{\Delta I_B})_{V_{CE}}}$$