資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學C++程式中的二分查詢？
二分查詢，也稱為半區間搜尋、對數搜尋或二分法，是一種搜尋演算法，用於在一個已排序的陣列中查詢目標值的位置。二分查詢將目標值與陣列的中間元素進行比較。如果它們不相等，則排除目標值不可能存在的半部分，並在剩餘的半部分繼續搜尋，再次取中間元素與目標值進行比較，並重復此過程，直到找到目標值。如果搜尋結束時剩餘部分為空，則目標值不在陣列中。儘管這個想法很簡單，但正確實現二分查詢需要關注一些關於其退出條件和中點計算的細微之處，特別是如果陣列中的值並非該範圍內所有整數時。
二分查詢是最流行的搜尋演算法。它效率高，也是解決問題的最常用技術之一。
如果將世界上所有姓名按順序排列在一起，並且您想搜尋特定姓名的位置，則二分查詢最多可在35次迭代中完成此操作。
二分查詢僅適用於已排序的元素集合。要在集合上使用二分查詢，必須先對集合進行排序。
當使用二分查詢對已排序集合執行操作時，可以根據被搜尋的值始終減少迭代次數。
讓我們考慮以下陣列：
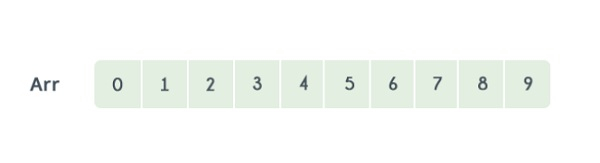
使用線性搜尋，將在第9次迭代中確定元素8的位置。
讓我們看看如何使用二分查詢減少迭代次數。在開始搜尋之前，我們需要知道範圍的起始位置和結束位置。我們稱它們為Low和High。
Low = 0 High = n-1
現在，將搜尋值K與位於下界和上界中位數的元素進行比較。如果值K更大，則增加下界，否則減少上界。
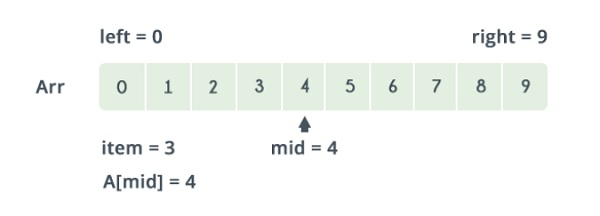
參考上圖，下界為0，上界為9。
下界和上界的中間值是 (lower_bound + upper_bound) / 2 = 4。這裡 a[4] = 4。值 4 > 2，這就是您要搜尋的值。因此，我們不需要對超過4的任何元素進行搜尋，因為超過4的元素顯然大於2。
因此，我們始終可以將陣列的上界降低到元素4的位置。現在，我們在同一個陣列上使用以下值遵循相同的過程：
Low: 0 High: 3
遞迴地重複此過程，直到 Low > High。如果在任何迭代中，我們得到 a[mid] = key，則返回 mid 的值。這是 key 在陣列中的位置。如果 key 不存在於陣列中，則返回 -1。
示例
int binarySearch(int low,int high,int key){
while(low<=high){
int mid=(low+high)/2;
if(a[mid]<key){
low=mid+1;
}
else if(a[mid]>key){
high=mid-1;
}
else{
return mid;
}
}
return -1; //key not found
}
778 次瀏覽
