大歐米茄（Ω）和大西塔（θ）表示法

漸近表示法

漸近表示法用於表示演算法的複雜度以進行漸近分析。這些表示法是表示複雜度的數學工具。有三種常用的表示法。

大歐米茄表示法

大歐米茄（Ω）表示法給出函式f(n)的常數因數內下界。

我們寫f(n) = Ω(g(n))，如果有正常數n₀和c，則n₀右方的f(n)始終位於c*g(n)之上或之上。

Ω(g(n)) = { f(n) : 對於所有n ≤ n₀，存在正常數c和n₀，使得0 ≤ c g(n) ≤ f(n)}

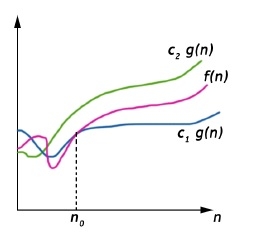
大西塔表示法

大西塔(Θ)表示法給出函式f(n)的常數因數內界限。

我們寫f(n) = Θ(g(n))，如果有正常數n₀和c₁和c₂ ，則n₀右方的f(n)始終 nằm giữa c₁*g(n)和c₂*g(n)包括。

Θ(g(n)) = {f(n) : 對於所有n ≥ n₀，存在正常數c₁、c₂和n₀，使得0 ≤ c₁ g(n) ≤ f(n) ≤ c₂ g(n)}

Arnab Chakraborty

更新於： 2019年8月5日

9K+ 瀏覽

啟動你 事業

透過完成課程獲得認證

立即開始