漸進複雜度

漸近分析

利用漸近分析，我們可以根據輸入規模瞭解演算法的效能。我們不應該計算確切的執行時間，而應該找到執行時間和輸入規模之間的關係。當輸入規模增加時，我們應該關注執行時間的變化。

對於空間複雜度，我們的目標是獲得一個關係或函式，描述演算法完成所需在主記憶體中佔用的空間量。

漸近行為

對於函式**f(n)**，漸近行為是指當n變大時f(n)的增長情況。不考慮小的輸入值。我們的任務是找到當輸入值很大時需要花費多少時間。

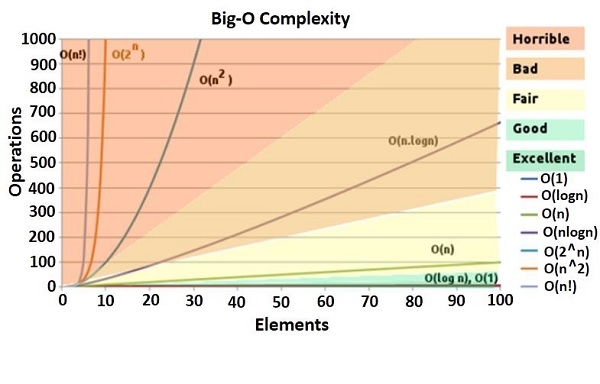
例如，f(n) = c * n + k 表示線性時間複雜度。f(n) = c * n² + k 表示二次時間複雜度。

演算法分析可以分為三種不同的情況。這些情況如下所示：

**最佳情況** - 在這裡計算執行時間的下界。它描述了演算法在最佳條件下的行為。

**平均情況** - 在這種情況下，我們計算演算法執行時間的上界和下界之間的區域。在這種情況下，執行的運算元量既不是最小也不是最大。

**最壞情況** - 在這種情況下，我們計算演算法執行時間的上界。在這種情況下，執行的運算元量最多。

Arnab Chakraborty

更新於： 2019年8月2日

5K+ 次瀏覽

開啟你的 職業生涯

透過完成課程獲得認證

開始學習