資料結構教程
網路教程
關係資料庫管理系統教程
作業系統教程
Java 教程
微軟 Excel 教程
iOS 教程
HTML 教程
CSS 教程
Android 教程
Python 教程
C 程式設計 教程
C++ 教程
C# 教程
MongoDB 教程
MySQL 教程
Javascript 教程
PHP 教程
物理學教程
化學教程
生物學教程
數學教程
英語教程
經濟學教程
心理學教程
社會學教程
時尚研究教程
法律研究教程漸近符號
漸近符號
漸近符號用來表示演算法的複雜度用於漸近分析。 這些符號是用於表示複雜度的數學工具。 一般來說使用三種符號。
大 O 符號
大 O（O）符號給出了到某一常數因子的函式 f(n) 的上限。
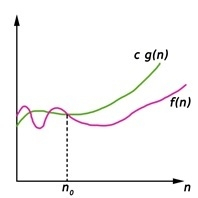
我們寫出 f(n) = O(g(n))，如果正數常數 n0 和 c 存在，對於大於 n0 的數，f(n) 總是落在 c*g(n) 上或其下方。
O(g(n)) = { f(n) : 存在正數常數 c 和 n0，對於大於或等於 n0 的任何 n，0 ≤ f(n) ≤ c g(n)}
大 Ω 符號
大 Ω（Ω）符號給出了到某一常數因子的函式 f(n) 的下限。
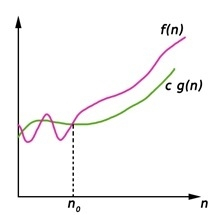
我們寫出 f(n) = Ω(g(n))，如果正數常數 n0 和 c 存在，對於大於 n0 的數，f(n) 總是落在 c*g(n) 上或其上方。
Ω(g(n)) = { f(n) : 存在正數常數 c 和 n0，對於大於或等於 n0 的任何 n，0 ≤ c g(n) ≤ f(n)}
大 Θ 符號
大Θ(Θ) 符號標註法能給出函式 f(n) 範圍的一個常量因子。
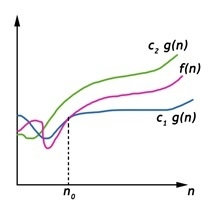
如果存在正數 n0 和 c1 以及 c2，使得在 n0 右側的 f(n) 時刻處於 c1*g(n) 與 c2*g(n) 之間（含）的話，我們寫為 f(n) = Θ(g(n))。
Θ(g(n)) = {f(n) : 存在正數 c1、c2 和 n0，使得對於所有 n ≥ n0，均有 0 ≤ c1 g(n) ≤ f(n) ≤ c2 g(n)}
更新於: 2023 年 10 月 21 日
29K+ 瀏覽量
廣告