資料結構
網路
關係型資料庫管理系統
作業系統
Java
Microsoft Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
JavaScript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究如何查詢圖是否是二分圖？
當圖中的頂點可以分成兩個獨立的集合，使圖中的每條邊要麼從第一個集合開始並結束於第二個集合，要麼從第二個集合開始並連線到第一個集合，換句話說，我們可以說在同一個集合中找不到邊，則該圖被稱為二分圖。
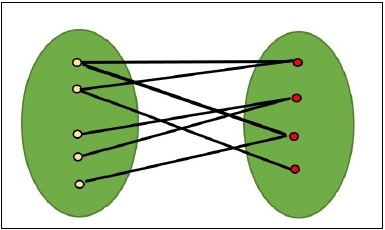
可以使用頂點著色來檢查二分圖。當一個頂點在同一個集合中時，它具有相同的顏色，對於另一個集合，顏色將改變。
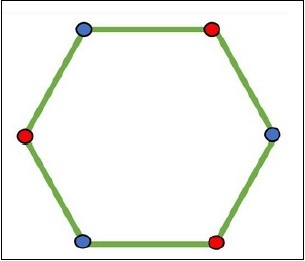
輸入和輸出
Input: The adjacency matrix. 0 1 1 1 0 0 1 0 0 1 1 0 1 0 0 1 0 1 1 1 1 0 1 1 0 1 0 1 0 1 0 0 1 1 1 0 Output: The graph is bipartite.
演算法
isBipartite(source)
輸入 − 源頂點。
輸出：當圖是二分圖時返回 True。
Begin define an empty queue qu, and a color list coloArray initially any node is not colored with any color color the source vertex as color red add source in the qu when qu is not empty, do remove item from the qu and take in u if there is any self-loop, then return false for all vertices v, which is connected with u, do if v has no color, then if colorArray[u] = red, then colorArray[v] := blue else if colorArray[u] = blue, then colorArray[v] := red add v into the queue if colorArray[v] = colorArray[u], then return false done done return true End
示例
#include<iostream>
#include<string>
#include<queue>
#define NODE 6
using namespace std;
/*int graph[NODE][NODE] = {
{0, 1, 1, 1, 0, 0},
{1, 0, 0, 1, 1, 0},
{1, 0, 0, 1, 0, 1},
{1, 1, 1, 0, 1, 1},
{0, 1, 0, 1, 0, 1},
{0, 0, 1, 1, 1, 0}
}; */
int graph[NODE][NODE] = {
{0, 1, 0, 0, 0, 1},
{1, 0, 1, 0, 0, 0},
{0, 1, 0, 1, 0, 0},
{0, 0, 1, 0, 1, 0},
{0, 0, 0, 1, 0, 1},
{1, 0, 0, 0, 1, 0}
};
bool isBipartite(int source) {
queue<int> qu;
string colorArray[NODE];
for(int i = 0; i< NODE; i++)
colorArray[i] = "No Color"; //initially no color is set for all vertices
colorArray[source] = "Red"; //assign red with the source vertex
qu.push(source); //add source into the queue.
while(!qu.empty()) {
int u = qu.front();
qu.pop();
if(graph[u][u] == 1) //there is a self loop
return false;
for(int v = 0; v < NODE; v++) {
if(graph[u][v] != 0 && colorArray[v] == "No Color") {
if(colorArray[u] == "Red") //assign adjacent list with alternate color
colorArray[v] = "Blue";
else if(colorArray[u] == "Blue")
colorArray[v] = "Red";
qu.push(v); //new adjacent node added to queue
} else if(graph[u][v] != 0 && colorArray[v] == colorArray[u]) {
return false; //when u and adjacent are of same color.
}
}
}
return true;
}
int main() {
bool check;
check = isBipartite(0);
if(check)
cout << "The graph is bipartite." << endl;
else
cout << "The graph is not bipartite." << endl;
} 輸出
The graph is bipartite.
更新於： 2020 年 6 月 16 日
4K+ 瀏覽
廣告