資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究機器學習中的威布林風險圖是什麼？
累積風險圖是一種圖形表示，幫助我們理解擬合到給定資料集的模型的可靠性。具體來說，它提供了對模型預期失效時間的洞察。
威布林分佈的累積風險函式描述了在特定時間段內累積的失效風險。簡單來說，它表示隨著時間推移累積的風險量，表明事件在該時間點之後發生的可能性。
透過檢視累積風險圖，我們可以瞭解所研究物件的失效模式和行為。它使我們能夠分析模型的可靠性並預測未來故障的時間。
什麼是威布林分佈？
為了研究物品或事件的可靠性和失效模式，可以使用一種稱為威布林分佈的數學模型。風險函式描述了未來事件發生的可能性。讓我舉一個例子來進一步說明這個概念。
假設一個手電筒已經使用了“t”時間。現在，風險函式使我們能夠計算手電筒在短時間視窗內失效的可能性，例如在使用 t 到 t + dt 小時之間。威布林風險函式提供了所述機率。如果我們檢視威布林風險圖，我們可以看到手電筒的風險函式是什麼樣的。在這種情況下，風險函式由公式 H(t) = (t/) 定義，其中和是威布林分佈特有的引數。
需要注意的是，威布林分佈的形狀引數（）的改變也會影響風險函式。不同的值會產生不同的風險函式，這些函式表示不同的風險或失效機率程度。總之，威布林風險函式使我們能夠理解事件在未來特定時間點發生的可能性。透過檢視風險圖，我們可以更多地瞭解物品或事件的可靠性和失效模式，這對於預測和控制風險很有幫助。
機器學習中的威布林風險圖是什麼？
威布林風險圖是機器學習中使用的圖形描述，用於評估處理事件時間或生存資料的模型的有效性和可靠性。它有助於我們理解事件或失效如何隨時間推移發展。讓我們舉一個假設情境，我們試圖預測某個事件何時發生，以便進一步解釋。例如，它可以是機器故障或客戶流失的剩餘時間。在這種情況下，威布林分佈通常用於模擬發生時間。
威布林風險圖以圖形方式顯示了擬合的威布林模型相關的風險函式。時間通常繪製在 x 軸上，而風險函式繪製在 y 軸上。風險函式描述了事件在特定時間點發生的風險或可能性。透過分析圖形中曲線的形狀和模式，我們可以更多地瞭解根據擬合的威布林模型，風險或失效率如何隨時間推移變化。此資訊有助於更容易地理解資料的行為和特性。
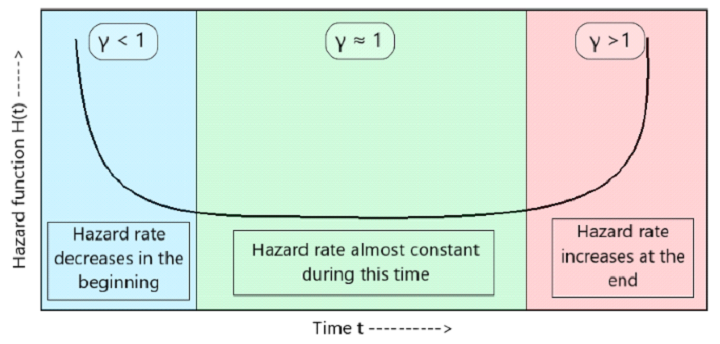
我們可以使用威布林風險圖來比較多個模型，或者評估不同因素如何影響風險函式。它還有助於根據擬合的威布林分佈預測未來潛在事件或失效可能發生的時間。總之，威布林風險圖是機器學習中一個有用的工具，有助於視覺化和分析生存資料。它使學者和行業專業人士能夠在瞭解風險、可靠性和事件或模型失效時間方面做出明智的決策。
威布林的 Python 示例
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import weibull_min
# Generate Weibull-distributed random data
shape = 2.5
scale = 50
data = weibull_min.rvs(shape, scale=scale, size=100)
# Sort the data in ascending order
sorted_data = np.sort(data)
# Compute the cumulative probability (CDF)
cdf = np.arange(1, len(sorted_data) + 1) / len(sorted_data)
# Compute the survival probability
survival_prob = 1 - cdf
# Create the Weibull plot
plt.figure(figsize=(8, 6))
plt.plot(sorted_data, cdf, marker='o', linestyle='-', label='Weibull Plot')
plt.xlabel('Time')
plt.ylabel('Cumulative Probability')
plt.title('Weibull Plot')
plt.legend()
plt.grid(True)
plt.show()
# Compute the hazard function
hazard = np.gradient(-np.log(survival_prob), sorted_data)
# Create the Weibull hazard plot
plt.figure(figsize=(8, 6))
plt.plot(sorted_data, hazard, marker='o', linestyle='-', color='r', label='Weibull Hazard Plot')
plt.xlabel('Time')
plt.ylabel('Hazard Function')
plt.title('Weibull Hazard Plot')
plt.legend()
plt.grid(True)
plt.show()
在此示例中，首先使用 'scipy.stats' 包中的 'weibull_min.rvs()' 方法生成基於威布林分佈的隨機資料。接下來，我們在按升序排序資料後計算累積機率 (CDF) 和生存機率。
威布林圖是第一個圖，由 'plt.plot()' 生成。x 軸是排序後的資料，y 軸是累積機率。使用 'plt.show()' 顯示兩個圖表。可以更改標籤、標題、網格線、顏色和其他繪圖引數以進一步滿足您的需求，以便進一步個性化繪圖的外觀。
132 次瀏覽
