使用平行四邊形定則求解給定物體的重量

---

引言

平行四邊形定則向量法有助於確定物體的方向，並有助於建立物體重量的概念。根據向量加法的平行四邊形定則，如果兩個向量可以用平行四邊形的相鄰邊來表示其大小和方向，那麼其合力的大小和方向可以用平行四邊形的對角線來表示。本教程將幫助您理解如果向量沿相同方向繪製，結果將顯示為平行四邊形的對角線。本教程的主要目的之一是透過力的定律來確定給定物體的重量。

平行四邊形定則向量

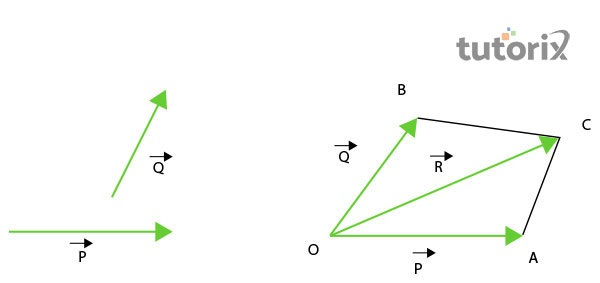
圖1：平行四邊形定則向量

平行四邊形是用於測量本教程中給出的不同材料的有用原理之一。平行四邊形定則指出，平行四邊形四邊長度的平方和等於兩條對角線長度的平方和。在歐幾里得幾何中，平行四邊形必須具有相等的對邊（Oller，2019）。例如，在本教程中，如果取ABCD為平行四邊形，則AB = DC且BC = AD。因此，平行四邊形的定義如下：$\mathrm{2(AB)^{2} + 2 (BC)^{2} = (AC)^{2} + (BD)^{2}}$。

所用材料

為了根據平行四邊形定則測量任何給定物體的重量，可以使用不同的材料。以下材料具有不同的用途，並有助於合成向量。想要進行計算的學生需要適當準備鉛垂線、待測重的物體、兩個帶刻度的砝碼盤。下一步，學生需要準備白紙、刻度尺、結實的細線和圖釘進行繪圖（Parween等人，2018）。此外，還需要反光鏡條和鉛筆來完成測量。

理論

$\mathrm{S\: = \:\sqrt{(P^{2}\: +\: Q^{2} \: +\: 2PQcos\theta)}}$

S為未知重量；P和Q為平衡砝碼重量

步驟

為了透過使用平行四邊形定則向量的實驗確定給定物體的重量，需要遵循以下步驟。需要將Gravesand裝置垂直放置在桌面上。必須確保滑輪處於良好工作狀態。需要用圖釘將一張白紙固定在滑輪之間（Zhang等人，2021）。將砝碼盤的鉤子系在細線的兩端。需要透過將另一根細線系在穿過滑輪的細線的中間來懸掛未知重量。

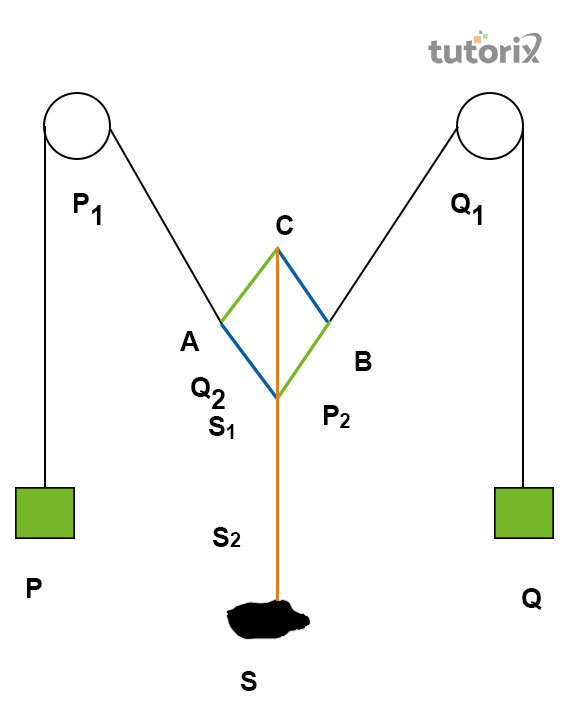
圖2：實驗圖

將帶刻度的砝碼掛在砝碼盤上，並調整砝碼的重量，直到結點到達紙張的中心。在每根細線下方放置一塊平面鏡，以確定力的方向。將眼睛放在細線覆蓋的地方，標記反光鏡條的末端。然後，將每對點連線起來，它們可以在O點相遇。然後標記OA和OB的邊。透過對角線連線標記點來測量OC，並使用彈簧秤來額外確保物體的重量。為了觀察實驗的重複性，需要多次更改連線在P點和Q點的砝碼重量。

觀察和計算

序號	力		邊長			合力R	未知重量S	彈簧秤測得的重量	誤差
	P	Q	OA	OB	OC
1.	145	145	3.5	3.5	3.6	180	200	205	5

表1：觀察表

彈簧秤的最小刻度和零點誤差將以克為單位確定（Cohen等人，2021）。所用刻度為1釐米，相當於50克。根據上述觀察表，發現OC = 3.6釐米，R = 50 × 3.6 = 180克。未知重量被認為等於200克，而平均未知重量計算為$\mathrm{S\:=\:\frac{S_{1}+S_{2}+S_{3}}{S} \:= \:200g}$。彈簧秤測得的重量與205克相似，差值為5克。

結論

本教程闡明瞭向量的一些因素，這些因素具有解決重量測量的潛在方程。大多數情況下，給定的材料是方程的有效部分，其中功能元件依賴於Gravesand裝置。基於力的平行四邊形定則，上述材料是有用的，需要包含具有功能元件的測量值，並且重量測量的建立遵循上面也提供的步驟。此外，還討論瞭如何透過應用向量平行四邊形定則以及觀察結果來觀察材料的重量。

常見問題

Q1. 在此實驗過程中需要注意哪些事項？

A1. 實驗板的位置需要穩定且垂直，滑輪必須具有較低的摩擦係數。紙張的中間需要有結點O，並且需要使用箭頭來表示方向。

Q2. 什麼是標量？

A2. 在物理學術語中，標量被定義為只有大小而沒有方向的物理量。