推薦系統中尋找相似性的技巧

---

簡介

相似度度量在推薦系統中至關重要，用於查詢具有相似行為、模式或品味的使用者。如今，推薦系統被廣泛應用於許多實用程式中，例如 Netflix 的電影推薦、電子商務和亞馬遜等平臺的產品推薦等。組織使用偏好矩陣來捕捉使用者對特定屬性產品的行為和反饋資料。他們還會捕捉使用者購買產品的順序和趨勢，並在過程中捕捉具有相似行為的使用者。

在本文中，讓我們簡要了解推薦系統背後的理念，並詳細探討相關的相似性技巧和度量。

什麼是推薦系統，它們有哪些型別？

推薦系統是一種機器學習演算法，它從流行的網站（如電子商務和電影網站）收集或使用使用者資料，這些資料涉及使用者行為，例如觀看歷史、點選、興趣和評分，並利用這些資料開發一個模型，該模型可以將具有相似興趣或喜好的使用者分組，向他們推薦產品或電影，甚至根據他們的活躍度對他們進行排名等。

推薦系統有兩種方法。

第一種是基於內容的演算法，第二種稱為協同過濾。

在**基於內容的方法**中，系統會捕捉使用者消費內容型別的資料。根據這些資料，演算法可以將來推薦相似的內容。

例如，一個觀看大量科幻電影的人，會根據模型捕捉到的他的興趣和喜好，獲得其他科幻電影的推薦。

在**協同過濾**中，演算法根據多個使用者的喜好向使用者推薦，而不是僅僅根據特定使用者消費的內容。

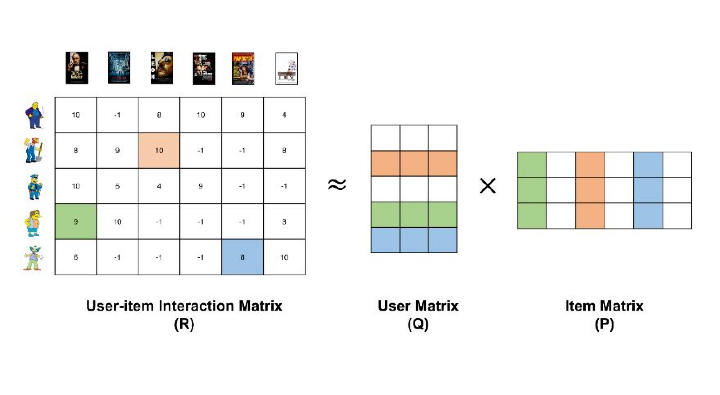
相似度矩陣

在協同過濾中，使用的方法是查詢相似的使用者。為此，演算法會根據使用者偏好生成一個矩陣。例如，讓我們以 Netflix 為例，四個使用者 A、B、C 和 D 觀看 7 部電影，如 GOT1、GOT2、GOT3、HP1、HP2、PB1 和 PB2，並對這些電影進行評分。空白行表示未評分。

	GOT1	GOT2	GOT3	HP1	HP2	PB1	PB2
A	5		5		5		4
B	4	3		5		4
C	4	4	4	3			4
D	4		5	5	5	5

上述矩陣稱為效用矩陣。

在此過程之後，計算相似度並生成相應的矩陣。

相似度矩陣可能如下所示

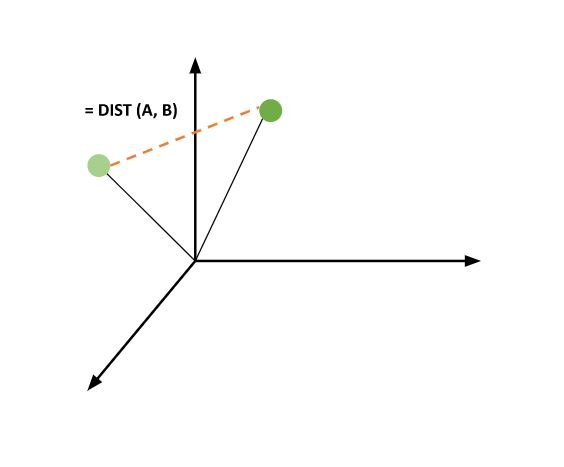
• **歐幾里得距離** - 它是兩個向量之間的距離，表示為

$\mathrm{d(x\:,\:y)\:= \sqrt{\:(\:x_{1}\:-\:y_{1}\:)^{2}\:\:+(\:x_{2}\:-\:y_{2}\:)^{2}\:\:+\:(\:x_{3}\:-\:y_{3}\:)\:^2+\:\ldots}\:+\:(x^{n}-y^{n})^{2}} $

例如，歐幾里得距離讓 A、B 和 C 為三個使用者，其向量為

A = [1,0,0,1,1]

B = [0,0,0,0,1]

C = [1,1,0,1,1]

$\mathrm{d(A\:,\:B)\:= \sqrt{\:(\:0_\:-\:1\:)^{2}\:\:+(\:0\:-\:0\:)^{2}\:\:+\:(\:0\:-\:0\:)\:^2+\: (\:0\:-\:1\:)\:^2+\:+ (\:1\:-\:1\:)\:^2}\:=\:\sqrt{2}\:=\:1.414}$

$\mathrm{d(A\:,\:B)\:= \sqrt{\:(\:1_\:-\:1\:)^{2}\:\:+(\:1\:-\:0\:)^{2}\:\:+\:(\:0\:-\:0\:)\:^2+\: (\:1\:-\:1\:)\:^2+\:+ (\:1\:-\:1\:)\:^2}\:=\:1}$

因此，從上面可以明顯看出，使用者 C 比使用者 B 更接近使用者 A。

因此，相似度與向量之間的距離成反比。

• **餘弦相似度** - 餘弦相似度衡量以零為起點兩個向量之間的角度。向量之間的角度越小，相似度越高。

在數學上，它可以表示為：

$\mathrm{SIM\:=\:\cos\theta\:=\frac{A\:\cdot\:B}{\:\rvert\rvert\:A\:\rvert\rvert\:\rvert\rvert\:B\:\rvert\rvert}\:=\:\frac{\displaystyle\sum\limits_{i=1}^n \:\:\:\:\:A_{i}B_{i}}{\sqrt{ \displaystyle\sum\limits_{i=1}^n A_{i}^2}\;\sqrt{\displaystyle\sum\limits_{i=1}^n B_{i}^2}}}$

在上述兩種度量中，歐幾里得度量原始距離度量，而餘弦距離和相似度也考慮了兩個向量的方向。因此，在查詢相似使用者時，餘弦相似度優於歐幾里得距離，因為我們考慮了使用者偏好。

結論

相似度度量是推薦系統的核心。有許多此類度量可用，然而，在所有這些度量中，歐幾里得距離和餘弦相似度是最廣泛使用的度量。歐幾里得距離度量空間中兩個向量之間的空間距離，而餘弦相似度度量兩個向量之間角度的餘弦，並且取決於空間中向量的方向和角度。這兩種方法在推薦系統中都非常有效。