資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究對稱最小最大堆
對稱最小最大堆 (SMMH) 定義為一棵完全二叉樹，其中除根節點外，每個節點都恰好包含一個元素。SMMH 的根節點可以為空，SMMH 中節點的總數為 m + 1，其中 m 是元素的數量。
設 y 為 SMMH 中的任意節點。設 elements(y) 為以 y 為根的子樹中的元素，但不包括 y 中的元素（如果有）。假設 elements(y) j= ∅。y 滿足以下屬性
- y 的左孩子在 elements(y) 中具有最小元素。
- y 的右孩子（如果有）在 elements(y) 中具有最大元素。
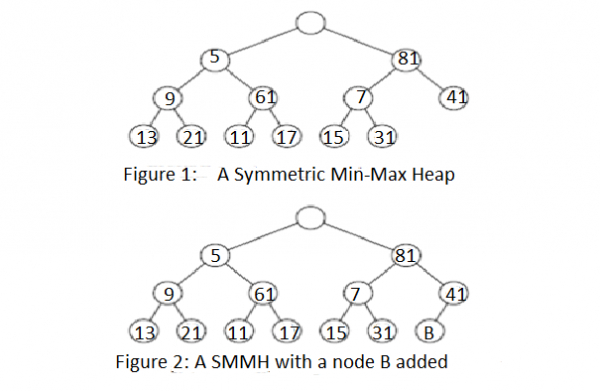
圖 1 顯示了一個包含 12 個元素的 SMMH 示例。
當 y 表示值為 81 的節點時，elements(y) = {7, 15, 31, 41}；y 的左孩子在 elements(y) 中具有最小元素 6；y 的右孩子在 elements(y) 中具有最大元素 41。我們可以驗證此 SMMH 的每個節點 y 都滿足所述屬性。
由於 SMMH 表示為一棵完全二叉樹，因此它儲存為一個隱式資料結構，實現了將完全二叉樹對映到陣列的標準方法。當 m = 1 時，最小和最大元素相同，幷包含在 SMMH 根節點的左孩子中。
當 m > 1 時，最小元素位於根節點的左孩子中，最大元素位於根節點的右孩子中。因此，getMin 和 getMax 操作消耗 O(1) 時間。
很容易看出，具有空根節點和每個其他節點中包含一個元素的 m + 1 個節點的完全二叉樹是 SMMH 當且僅當以下條件為真 -
A1 - 對於每個具有右兄弟的節點 y，y 中的元素小於或等於其右兄弟中的元素。
A2 - 對於每個具有祖父母節點的節點 y，祖父母節點的左孩子中的元素小於或等於 y 中的元素。
A3 - 對於每個具有祖父母節點的節點 y，祖父母節點的右孩子中的元素大於或等於 y 中的元素。
請注意，如果屬性 A1 在節點 y 處滿足，則在 y 處最多隻有一個 A2 和 A3 可能被違反。透過實現屬性 A1 到 A3，我們得到了用於插入和刪除元素的簡單演算法。這些演算法是對最小堆和最大堆的相應演算法的簡單改編。它們的複雜度為 O(log m)。
這裡，我們指定插入操作。假設我們希望將 3 插入到圖 1 的 SMMH 中。由於 SMMH 是一棵完全二叉樹，因此我們必須在圖 2 所示的位置向 SMMH 新增一個新節點；新節點標記為 B。
在我們的示例中，B 將表示一個空節點。現在 3 插入到節點 B 中。
1K+ 次檢視
