資料結構中的稀疏矩陣

在本節中，我們將瞭解什麼是稀疏矩陣以及如何在記憶體中表示它們。如果矩陣的大部分元素為0，則該矩陣為稀疏矩陣。另一個定義是，非零元素最多為1/3（大約m x n的30%）的矩陣稱為稀疏矩陣。

我們在計算機記憶體中使用矩陣以高效的方式執行某些操作。但是，如果矩陣本質上是稀疏的，它可能有助於我們高效地執行操作，但它會在記憶體中佔用更大的空間。這些空間毫無用處。因此，我們將遵循其他型別的結構來儲存稀疏矩陣。

假設我們有一個如下所示的稀疏矩陣：

我們可以看到有8個非零元素和28個零值。此矩陣佔用6*6 = 36個記憶體空間。如果矩陣的大小更大，則空間浪費將會增加。

我們可以使用表結構來儲存有關稀疏矩陣的資訊。假設我們將建立一個名為X的表，如下所示：

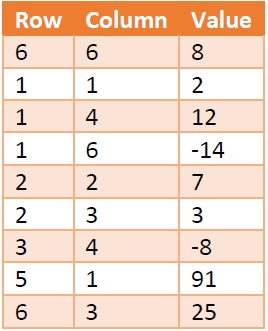
這裡，第一列儲存行號，第二列儲存列號。第三列儲存M[row, col]中存在的資料。此表的每一行都稱為三元組，因為有三​​個引數。第一個三元組儲存矩陣的大小資訊。Row = 6和Column = 6表示矩陣M是6 x 6矩陣。value欄位表示陣列中存在的非零元素的數量。

此表也佔用9 * 3 = 36個空間，那麼優勢在哪裡呢？如果矩陣大小為8*8 = 64，但只有8個元素，那麼表X也將佔用36個單元的空間。我們可以看到有固定的3列，行數隨非零元素的數量而變化。因此，如果有T個非零元素，則空間複雜度將為O(3*T) = O(T)。對於矩陣，它將是O(m x n)。

更新於：2020年8月10日

5K+ 次瀏覽

開啟你的職業生涯

完成課程獲得認證

開始學習
廣告