四分位數

---

介紹

在統計學中，三個主要術語用於描述資料的集中趨勢，即平均數、中位數和眾數。但是，這些術語指的是代表中心值的特定數字。然而，四分位數是另一個統計術語，用於比上述術語更有效地描述資料。四分位數的概念通常用於比較一家公司的的資料與另一家公司的的資料。此外，它還用於以圖形方式表示中位數和四分位數。在本教程中，我們將學習關於四分位數的定義、公式、偏差、範圍以及一些相關的解題示例。

定義

四分位數定義為一種分位數類別，它將一個組分成四個部分或四分之一。分位數是將連續分佈分成相等機率的切割點。它們是一種百分位數。四分位數有三個點，例如第一（Q₁）、第二（Q₂）和第三（Q₃）四分位數。此外，第二四分位數（Q₂）是其餘兩個四分位數的中位數。為了找到資料集的四分位數，需要將資料按升序排列。

公式

存在用於確定資料集四分位數的公式。使用公式，我們可以確定第一（位於第一項和中位數之間）、第二（中位數）和第三四分位數（位於中位數和最後一項之間）。在計算之前，應將資料集按升序排列。計算給定資料集四分位數的公式如下：

• 第一四分位數（Q₁）或下四分位數：$\mathrm{(\frac{m+1}{4})^{th}}$ 項

• 第二四分位數（Q₂）或四分位間距：$\mathrm{(\frac{m+1}{2})^{th}}$ 項

• 第三四分位數（Q₃）或上四分位數：$\mathrm{(\frac{3(m+1)}{4})^{th}}$ 項

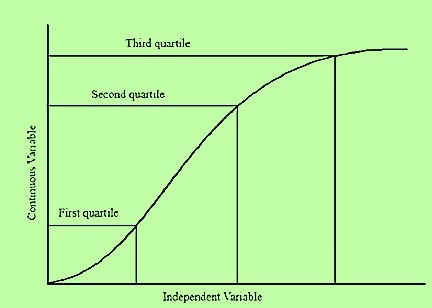
統計學中的四分位數

我們已經看到，四分位數將組分成四個部分。每個部分都位於特定範圍內。因此，每個四分位數的範圍如下所述。

符號	四分位數名稱	範圍
Q1	第一或下四分位數	將最低的 25% 與整個資料分開
Q2	第二四分位數或中位數	位於中位數值上，這意味著它將資料分成兩半
Q3	第三或上四分位數	將最高的 25% 與整個資料分開

四分位差

它被定義為一種統計度量，它使用平均值來評估資料的偏差。換句話說，它確定了資料的平均值。它說明了分佈的散佈情況。它也稱為**半四分位間距**。在數學上，它可以表示為：

四分位差 $\mathrm{= \frac{Q_3-Q_1}{2}}$

其中 Q₃-Q₁ 是四分位間距。

四分位差可以針對分組資料和非分組資料確定。讓我們討論評估四分位差的過程。

• 第一步，對於分組資料和非分組資料，都將資料按升序排列。

• 使用以下公式評估第一四分位數：

  非分組資料：$\mathrm{(Q_1) (\frac{m+1}{4})^{th}}$ 項

  分組資料： $\mathrm{Q_1=p_1+\frac{\frac{N}{4}-c}{f}(p_2-p_1)}$

  其中 m 是四分位數的數量。此外，p₁ 和 p₂ 是資料的下限和上限。N、f 和 c 分別是總頻數、特定類別的頻數和累積頻數。

• 使用以下公式查詢第三四分位數：

  非分組資料： $\mathrm{(Q_3) \:\: (\frac{3(m+1)}{4})^{th}}$ 項

  分組資料： $\mathrm{Q_3=p_1+\frac{\frac{3N}{4}-c}{f}(p_2-p_1)}$

• 現在，我們可以使用公式確定四分位差，如下所示：

  四分位差 = $\mathrm{= \frac{Q_3-Q_1}{2}}$

四分位間距

四分位間距是第一四分位數和第三四分位數之間的差。它衡量資料的散佈情況，這意味著它衡量資料集中間 50% 的資料。

評估四分位間距的數學表示式為：

$$\mathrm{四分位間距 = Q_3-Q_1=(\frac{3(m+1)}{4})^{th} 項-(\frac{(m+1)}{4})^{th} 項 }$$

讓我們討論評估四分位間距的過程。

• 步驟 1：對於分組資料和非分組資料，都將資料按升序排列。

• 步驟 2：使用以下公式查詢資料集的中位數（Q₂）。

  對於偶數資料集： $\mathrm{Q_2=\frac{(\frac{n}{2})^{th} 項+(\frac{n}{2}+1)^{th} 項}{2}}$

  對於奇數資料集： $\mathrm{Q_2=(\frac{n+1}{2})^{th} 項}$

• 步驟 3：查詢四分位數 Q₁，它是步驟 2 中找到的中位數左側資料點的中位數。

• 步驟 4：查詢四分位數 Q₃，它是步驟 2 中找到的中位數右側資料點的中位數。

  四分位間距 = Q₃-Q₁

解題示例

示例 1

評估以下資料集的中位數、下四分位數、上四分位數和四分位間距：

23, 56, 110, 12, 6, 89, 103

我們必須將資料集按升序排列，如下所示：

6, 12, 23, 56, 89, 103, 110

由於元素的數量為奇數（即 7），因此中位數 $\mathrm{=(\frac{7+1}{2})^{th} 項=12}$

第一四分位數（Q₁）或下四分位數：=$\mathrm{(\frac{m+1}{4})^{th} 項=(\frac{7+1}{4})^{th} 項=56}$

第三四分位數（Q₃）或上四分位數： $\mathrm{(\frac{3(m+1)}{4})^{th} 項=(\frac{3(7+1)}{4})^{th} 項=89}$

四分位間距 =Q₃-Q₁=89-56=33

∴ 以下資料集的中位數、下四分位數、上四分位數和四分位間距分別為 12、56、89 和 33。

示例 2

查詢以下資料集的四分位差和四分位間距：

8, 20, 5, 16, 49, 32, 78, 56, 11, 39, 1

解答

我們必須將資料集按升序排列，如下所示：

1, 5, 8, 11, 16, 20, 32, 39, 49, 56, 78

由於元素的數量為奇數（即 11），因此中位數 =$\mathrm{(\frac{11+1}{2})^{th} 項= 32}$

第一四分位數（Q_1）或下四分位數：=$\mathrm{(\frac{m+1}{4})^{th} 項=(\frac{11+1}{4})^{th} 項=5}$

第三四分位數（Q_3）或上四分位數： $\mathrm{(\frac{3(11+1)}{4})^{th} 項=(\frac{3(11+1)}{4})^{th} 項=11}$

四分位差 $\mathrm{= \frac{Q_3-Q_1}{2}=\frac{11-5}{2}=3 }$

現在，四分位間距 $\mathrm{=Q_3-Q_1=11-5=6}$

∴ 資料集的四分位差和四分位間距分別為 3 和 6。

結論

本教程簡要介紹了四分位數及其在統計學中的應用。此外，還說明了與四分位差和四分位間距相關的基本公式。此外，還提供了一些解題示例，以便更好地理解這個概念。總之，本教程可能有助於理解四分位數的基本概念。

常見問題

1. 如何確定四分位差係數？

四分位差係數可以使用以下表達式確定 $\mathrm{\frac{Q_3-Q_1}{Q_3+Q_1}}$。

2. 標準差和四分位差有什麼區別？

當給出極端異常值時，標準差用於測量資料的離散程度。如果沒有提供極端異常值，則應使用四分位差來確定資料的分佈散佈。

3. 四分位數有哪些應用？

四分位數是一種統計工具，用於建立資料集的箱線圖。此外，它有助於比較一家公司的的資料與另一家公司的的資料。

4. 哪個四分位數被稱為資料集的中位數？

第二四分位數是資料集的中位數。

5. 哪個區域屬於第一四分位數？

第一四分位數將資料集的前 25% 與後 75% 分開。