資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究C++ 實現部分填充數獨格子的程式
假設我們有一個部分填充的數獨網格，我們需要解決它。我們知道數獨是一個 9 × 9 的數字網格，整個網格也分成 3 × 3 的小方格。有一些規則需要遵循來解決數獨。
我們需要使用數字 1 到 9 來解決這個問題。
同一行、同一列或同一 3 × 3 小方格內不能重複出現相同的數字。
我們將使用回溯演算法來解決數獨問題。當某個單元格填充了一個數字後，它會檢查該數字是否有效。如果無效，則會檢查其他數字。如果檢查了 1−9 之間的所有數字，並且沒有找到有效的數字來放置，則回溯到之前的選項。
所以如果輸入如下所示：
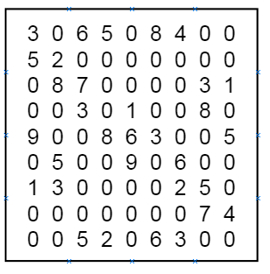
輸出將是：
為了解決這個問題，我們將遵循以下步驟：
定義一個名為 isPresentInCol() 的方法，它將接收列和數字作為引數
對於網格中的每一行 r，執行以下操作：
如果 grid[r, col] 等於 num，則返回 true
否則返回 false
定義一個名為 isPresentInRow() 的方法，它將接收行和數字作為引數
對於網格中的每一列 c，執行以下操作：
如果 grid[row, c] 等於 num，則返回 true
否則返回 false
定義一個名為 isPresentInBox() 的方法，它將接收小方格起始行、小方格起始列和數字作為引數
對於從 boxStartRow 開始到接下來的 3 行的每一行 r，執行以下操作：
對於從 boxStartCol 開始到接下來的 3 列的每一列 r，執行以下操作：
如果 grid[r, c] 等於 num，則返回 true
否則返回 false
定義一個名為 findEmptyPlace() 的方法，它將接收行和列作為引數
對於網格中的每一行 r，執行以下操作：
對於網格中的每一列 c，執行以下操作：
如果 grid[r, c] 等於 0，則返回 true
返回 false
定義一個名為 isValidPlace() 的方法，它將接收行、列和數字作為引數
如果 isPresentInRow(row, num)、isPresentInCol(col, num) 和 isPresntInBox(row − row mod 3, col − col mod 3, num) 全部返回 false，則返回 true
定義一個名為 solveSudoku() 的方法，它將接收網格作為引數
如果網格中沒有空位置，則返回 true
對於數字 1 到 9，執行以下操作：
如果 isValidPlace(row, col, number) 返回 true，則：
grid[row, col] := number
如果 solveSudoku 返回 true，則返回 true
grid[row, col] := 0
返回 false
讓我們看下面的實現來更好地理解：
示例
#include <iostream>
#define N 9
using namespace std;
int grid[N][N] = { {3, 0, 6, 5, 0, 8, 4, 0, 0},
{5, 2, 0, 0, 0, 0, 0, 0, 0},
{0, 8, 7, 0, 0, 0, 0, 3, 1},
{0, 0, 3, 0, 1, 0, 0, 8, 0},
{9, 0, 0, 8, 6, 3, 0, 0, 5},
{0, 5, 0, 0, 9, 0, 6, 0, 0},
{1, 3, 0, 0, 0, 0, 2, 5, 0},
{0, 0, 0, 0, 0, 0, 0, 7, 4},
{0, 0, 5, 2, 0, 6, 3, 0, 0}};
bool isPresentInCol(int col, int num){
//check whether num is present
in col or not
for (int row = 0; row < N; row++)
if (grid[row][col] == num)
return true;
return false;
}
bool isPresentInRow(int row, int num){
//check whether num is present
in row or not
for (int col = 0; col < N; col++)
if (grid[row][col] == num)
return true;
return false;
}
bool isPresentInBox(int boxStartRow, int boxStartCol, int num){
//check whether num is present in 3x3 box or not
for (int row = 0; row < 3; row++)
for (int col = 0; col < 3; col++)
if (grid[row+boxStartRow][col+boxStartCol] == num)
return true;
return false;
}
void sudokuGrid(){
//print the sudoku grid after solve
for (int row = 0; row < N; row++){
for (int col = 0; col < N; col++){
if(col == 3 || col == 6)
cout << " | ";
cout << grid[row][col] <<" ";
}
if(row == 2 || row == 5){
cout << endl;
for(int i = 0; i<N; i++)
cout << "---";
}
cout << endl;
}
}
bool findEmptyPlace(int &row, int &col){
//get empty location and
update row and column
for (row = 0; row < N; row++)
for (col = 0; col < N; col++)
if (grid[row][col] == 0) //marked with 0 is empty
return true;
return false;
}
bool isValidPlace(int row, int col, int num){
//when item not found in col, row and current 3x3 box
return !isPresentInRow(row, num) && !isPresentInCol(col, num) &&
for (int row = 0; row < N; row++){
for (int col = 0; col < N; col++){
if(col == 3 || col == 6)
cout << " | ";
cout << grid[row][col] <<" ";
}
if(row == 2 || row == 5){
cout << endl;
for(int i = 0; i<N; i++)
cout << "−−−";
}
cout << endl;
}
}
bool findEmptyPlace(int &row, int &col){
//get empty location and
update row and column
for (row = 0; row < N; row++)
for (col = 0; col < N; col++)
if (grid[row][col] == 0) //marked with 0 is empty
return true;
return false;
}
bool isValidPlace(int row, int col, int num){
//when item not found in col, row and current 3x3 box
return !isPresentInRow(row, num) && !isPresentInCol(col, num) &&
cout << "No solution exists";
}輸入
{3, 0, 6, 5, 0, 8, 4, 0, 0},
{5, 2, 0, 0, 0, 0, 0, 0, 0},
{0, 8, 7, 0, 0, 0, 0, 3, 1},
{0, 0, 3, 0, 1, 0, 0, 8, 0},
{9, 0, 0, 8, 6, 3, 0, 0, 5},
{0, 5, 0, 0, 9, 0, 6, 0, 0},
{1, 3, 0, 0, 0, 0, 2, 5, 0},
{0, 0, 0, 0, 0, 0, 0, 7, 4},
{0, 0, 5, 2, 0, 6, 3, 0, 0}輸出
3 1 6 | 5 7 8 | 4 9 2 5 2 9 | 1 3 4 | 7 6 8 4 8 7 | 6 2 9 | 5 3 1 --------------------------- 2 6 3 | 4 1 5 | 9 8 7 9 7 4 | 8 6 3 | 1 2 5 8 5 1 | 7 9 2 | 6 4 3 --------------------------- 1 3 8 | 9 4 7 | 2 5 6 6 9 2 | 3 5 1 | 8 7 4 7 4 5 | 2 8 6 | 3 1 9
263 次瀏覽
