資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學C語言中約簡形式的N個分數的乘積
給定N個分數的分子num和分母den，任務是找到N個分數的乘積，並且輸出結果應為約簡形式。
例如，在下圖中，我們有兩個分數“4/5”和“3/4”，我們找到了這兩個分數的乘積，其中第一個分數的分子乘以第二個分數的分子，第一個分數的分母乘以第二個分數的分母。現在的最終結果是“12/20”，可以約簡，所以輸出應該是“3/5”，同樣，我們必須開發一個程式來解決給定的問題。
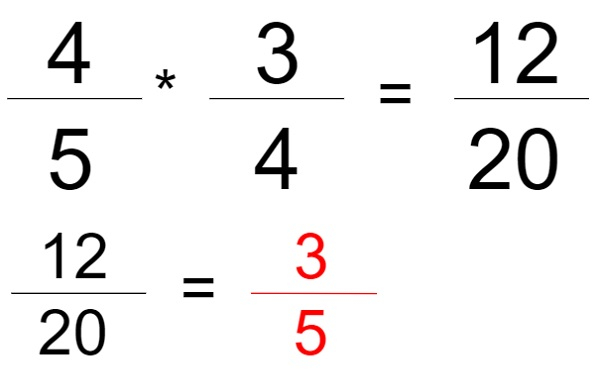
輸入
fraction f[3] = {{1,2},
{2,1},
{5,6}}輸出
5/6
說明 − 1/2 * 2/1 * 5/6 = 10/12，可以約簡為 5/6。
輸入
fraction f[2] = {{2, 3},
{1,4}}輸出
1/6
說明 − 2/3 * 1/4 = 2/12，可以約簡為 1/6
下面使用的解決問題的方法如下
為了解決上述問題，我們可以將所有分母和分子相乘，將結果儲存在另一個變數prod_den和prod_num中，它們將分別成為最終分母和最終分子，現在我們必須找到約簡形式，為此我們必須找到prod_num和prod_den的GCD（最大公約數），並用它們各自的GCD除以prod_num和prod_den。
演算法
Start
Declare a struct fraction with following elements
1. num, 2. den
In function int GCD(int a, int b)
Step 1→ If a == 0 then,
Return b
Step 2→ Return GCD(b % a, a)
In function int product(int n, fraction f[])
Step 1→ Initialize prod_num = 1 prod_den = 1
Step 2→ Loop For i = 0; i < n; i++
prod_num = prod_num * f[i].num
prod_den = prod_den * f[i].den
Step 3→ Declare and initialize gcd = GCD(prod_num, prod_den)
Step 4→ prod_num = prod_num / gcd
Step 5→ prod_den = prod_den / gcd
Step 6→ Print prod_num, prod_den
In Function int main()
Step 1→ Declare struct fraction f[3] = {
{1,2},
{2,1},
{5,6}}
Step 2→ Declare and initialization n as sizeof(f)/sizeof(f[0])
Step 3→ product(n, f)
Stop示例
#include <stdio.h>
struct fraction{
int num;
int den;
};
// Function to return gcd of a and b
int GCD(int a, int b){
if (a == 0)
return b;
return GCD(b % a, a);
}
//fucntion to print the result
int product(int n, fraction f[]){
int prod_num = 1, prod_den = 1;
// finding the product of all N
// numerators and denominators.
for (int i = 0; i < n; i++) {
prod_num *= f[i].num;
prod_den *= f[i].den;
}
// Finding GCD of new numerator and
// denominator
int gcd = GCD(prod_num, prod_den);
// finding reduced form
prod_num /= gcd;
prod_den /= gcd;
printf("%d/%d
", prod_num, prod_den);
return 0;
}
int main(){
struct fraction f[3] = {
{1,2},
{2,1},
{5,6}};
int n = sizeof(f)/sizeof(f[0]);
product(n, f);
return 0;
}輸出
如果執行上述程式碼，它將生成以下輸出：
5/6
更新於：2020年8月13日
158 次瀏覽
廣告