一個半徑為 50 釐米的空心鋁球的閃亮外表面將用作鏡子：(a) 該鏡子的焦距是多少？(b) 它將提供哪種型別的球面鏡？(c) 說明該球面鏡會發散還是會聚光線。

(a) 已知

鏡子的曲率半徑，$R$ = 50 釐米。

我們知道焦距 $f$ 等於曲率半徑 $R$ 的一半，表示為

$f=\frac {1}{2} \times {R}$

現在，將 $R$ 的值代入上式，得到：

$f=\frac {1}{2} \times {50}$

$f=25cm$

因此，該鏡子的焦距為 25 釐米。

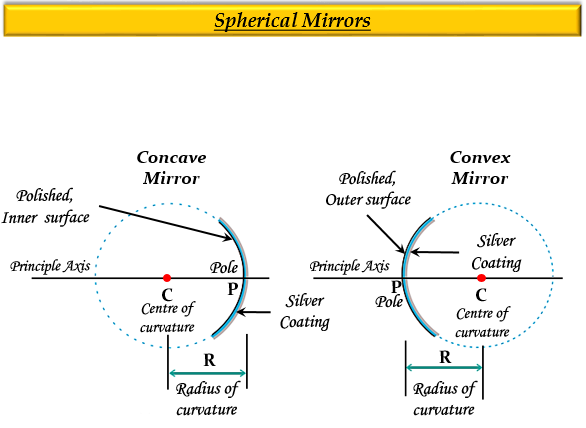
(b) 由於外表面是閃亮的，因此它將提供一個 凸面鏡。

(c) 該球面鏡會使光線發散。

解釋

如果一個球面鏡的內表面是閃亮的或拋光的，則它是一個凹面鏡，而如果一個球面鏡的外表面是閃亮的或拋光的，則它是一個凸面鏡。

凹面鏡會聚光線，因此也被稱為會聚鏡，而凸面鏡使光線發散，也被稱為發散鏡。

教程點

更新於： 2022 年 10 月 10 日

5K+ 次檢視

開啟你的 職業生涯

完成課程獲得認證

立即開始