在數軸上表示$\frac{4}{3}$和$\frac{-2}{9}$。
已知
$\frac{4}{3}$ 和 $\frac{-2}{9}$。
要求
我們需要在數軸上表示$\frac{4}{3}$和$\frac{-2}{9}$。
解答
$\frac{4}{3}$
為了在數軸上表示分數,我們需要將兩個整數之間的線段分成'n'個相等的部分,其中n表示分數的分母。
因此,
如果我們必須在數軸上表示分數$\frac{4}{3}=1\frac{1}{3}$,我們需要將1和2之間的線段分成三個相等的部分。
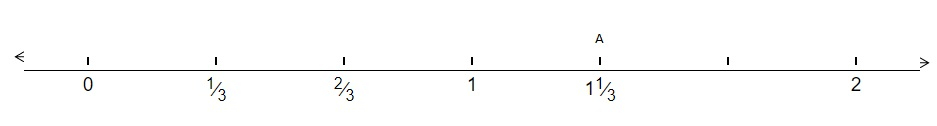
點A是所需點。
$\frac{-2}{9}$
畫一條數軸。
由於數字$\frac{-2}{9}$是一個負數,因此它將在0的左側。它位於$0$和$-1$之間。
將$0$和$-1$之間的線段分成9個部分(這裡9是分母)。
A是所需點。
- 相關文章
- 在數軸上表示數字$\frac{2}{4}$。
- 在數軸上表示\( \frac{-2}{11}, \frac{-5}{11}, \frac{-9}{11} \)。
- 在數軸上表示$\frac{-5}{4}$。
- 在數軸上表示$\frac{10}{3}$。
- 在數軸上表示數字$\frac{7}{4}$。
- 在數軸上表示以下數字:(i)$\frac{-4}{7}$(ii)$\frac{-2}{5}$
- 在數軸上表示$\frac{16}{3}$。
- 如何在數軸上比較$\frac{5}{4}$和$\frac{2}{3}$?
- 如何在數軸上表示有理數?在數軸上表示$\frac{-4}{3}$。
- 在數軸上表示以下數字:$\frac{-2}{6}$
- 畫一條數軸,並在其上標出以下點:$\frac{1}{2}, \frac{1}{4}, \frac{3}{4}, \frac{4}{4}$
- 在數軸上表示$\frac{-14}{15}$。
- 在數軸上表示這些數字。(i)\( \frac{7}{4} \)(ii)\( \frac{-5}{6} \)。
- 畫出數軸,並在其上表示以下有理數:(i)$\frac{3}{4}$(ii)$\frac{-5}{8}$(iii)$\frac{-7}{4}$(iv)$\frac{7}{8}$
- 在數軸上顯示以下數字。每個例子都畫一條單獨的數軸。(1)$\frac{3}{2}, \frac{5}{2},-\frac{3}{2}$。(2)$\frac{7}{5}, \frac{-2}{5}, \frac{-4}{5}$。(3)$\frac{-5}{8}, \frac{11}{8}$。(4)$\frac{13}{10}, \frac{-17}{10}$。
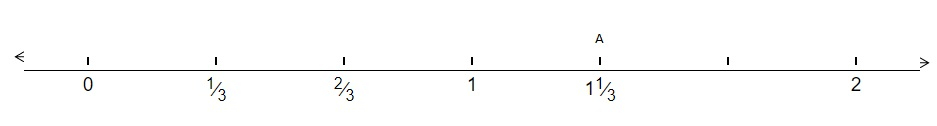



 資料結構
資料結構 網路
網路 關係資料庫管理系統 (RDBMS)
關係資料庫管理系統 (RDBMS) 作業系統
作業系統 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C語言程式設計
C語言程式設計 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP