資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究根據給定的圖形，求出距離和位移。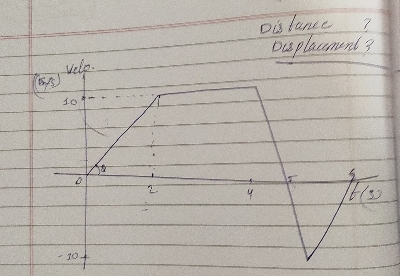
"\n
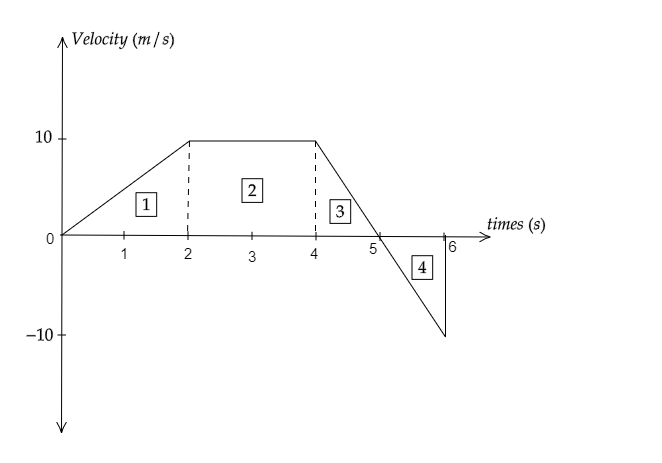
距離=三角形1的面積+矩形2的面積+三角形3的面積+三角形4的面積
$=\frac{1}{2}\times2\times10+2\times10+\frac{1}{2}\times1\times10+\frac{1}{2}\times1\times10$
$=10+20+5+5$
$=40$
因此，距離$=40\ m$
對於位移
在 $\boxed{1}$ 中，速度變化 $\Delta v=v_2-v_1=10-0=10\ m$
時間變化 $\Delta t=t_2-t_1=2-0=2\ s$
因此，位移 $d_1=\Delta v\times\Delta t=10\times2=20\ m$
在 $\boxed{2}$ 中，速度均勻，
所以，速度變化 $\Delta v=v_2-v_1=10-10=0$
時間變化 $\Delta t=t_2-t_1=4-2=2$
所以，位移 $d_2=\Delta v\times\Delta t=0\times2=0$
在 $\boxed{3}$ 中，
速度變化 $\Delta v=v_2-v_1=0-10=-10\ m/s$
時間變化 $\Delta t=t_2-t_1=5-4=1\ s$
所以，位移 $d_3=\Delta v\times \delta t=-10\times1=-10\ m$
在 $\boxed{4}$ 中，
速度變化 $\Delta v=v_2-v_1=-10-0=-10\ m/s$
時間變化 $\Delta t=t_2-t_1=6-5=1\ s$
所以位移 $d_4=\Delta v\times\Delta t$
$=-10\times1=-10\ m$
圖中總位移$=d_1+d_2+d_3+d_4$
$=20+0-10-10$
$=0$
因此，從給定的圖形中，我們發現總距離$=40\ m$，位移$=0$。
38 次瀏覽
