最小化顏色以繪製圖，使得沒有路徑具有相同的顏色

圖著色是圖論中圖示記的一個子集。顏色的使用源於地圖上國家的著色，其中每個區域都著色。圖著色有幾個現實世界的應用，以及理論問題。除了傳統形式的問題外，還可以對圖、著色方式甚至顏色本身施加其他約束。它甚至以著名的數字謎題數獨的形式獲得了廣泛的關注。圖著色仍然是一個活躍的研究領域。

什麼是頂點著色？

頂點著色是指為任何圖的每個頂點或節點分配顏色或標籤，使得沒有兩個顏色相同的節點透過邊連線。最流行的頂點著色方法試圖減少單個圖中使用的顏色數量。這種型別的著色稱為最小頂點著色。

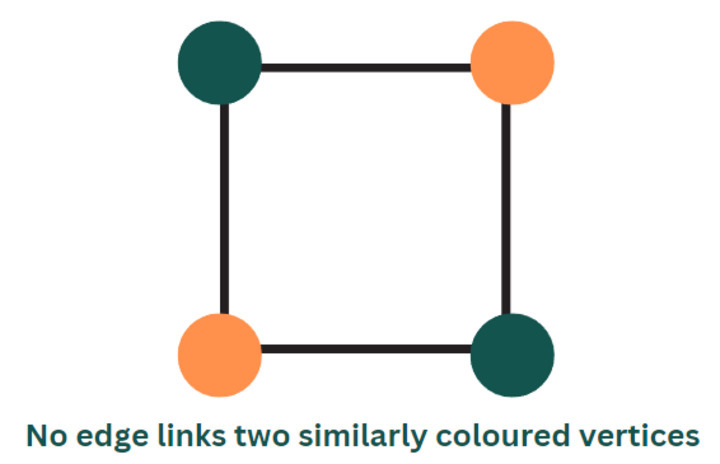
k-著色是指使用k種或更少顏色對圖進行頂點著色。k-可著色圖採用色數k，色數為k的圖稱為“k-色圖”。唯一一種單色可著色（因此是單色）的圖是空圖，而雙色可著色圖包括二分圖。四色定理指出所有平面圖都是4-可著色的。

邊著色

當為圖的邊分配不同的顏色時，確保沒有節點旁邊有兩個以上相同顏色的邊，則稱為邊適當著色。圖的色指數或邊色數是指用於邊著色的最小顏色數量。

色數

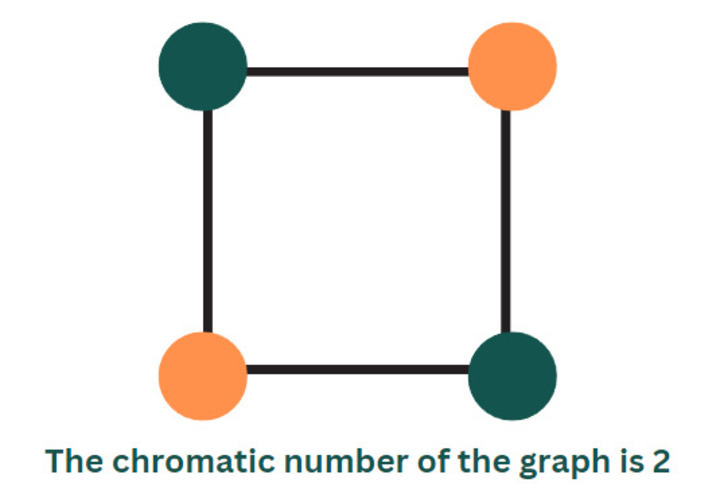
色數定義為用於對任何圖的頂點或節點進行著色的最小顏色數。此數字的值通常大於一。另一方面，當圖只有一個頂點時，色數為一。

如何最小化顏色以著色圖，其中沒有路徑具有相同的顏色？

以下是一個基於拓撲排序理論的解決方案：

在“有向無環圖 (DAG)”中，拓撲排序定義為節點的“線性排序”，這樣對於任何有向邊（例如，p，q），p頂點在排列中出現在q之前。

如果圖不是DAG，則拓撲排序不可行

在拓撲排序中，

  • “使用一個臨時堆疊”。

  • “不要立即顯示頂點；而是先在其每個相鄰頂點上遞迴執行拓撲排序，然後再將其壓入堆疊”。

  • “最後，列印堆疊的內容”。

我們可以看到，所需的最小顏色數等於圖的最長路徑的長度。

所有入度等於零的節點都可以具有相同的顏色。從它們的鄰居中消除一個入度，並迴圈遍歷所有入度 = 0 的節點。

“如果遵循此規則，則只有在所有路徑中位於其上方的每個節點都被分配了顏色之後，才會為特定節點分配顏色。因此，這將提供路徑的最長可能長度”。

要將這個想法付諸實踐，請遵循以下步驟：

  • 根據提供的邊，構建有向圖的鄰接表。

  • 保留一個入度向量，其中包含每個節點的入度。

  • 宣告一個變數（例如，depth）來儲存節點的深度。

  • “在拓撲排序的每次迭代期間，選擇一種新顏色並將其分配給入度為 0 的節點，並且當新增新顏色時，深度增加一”。

  • 作為必要的答案，返回深度的最終值。

示例

#include <bits/stdc++.h>
using namespace std;
  
// Function to find minimum number of colours required
int min_colour(int N, int M, vector<int> mat[]){

   // Create an adjacency list
   vector<vector<int> > adj(N + 1);
  
   // Create indeg to store indegree of every minion
   vector<int> indeg(N + 1);
  
   for (int i = 0; i < M; i++) {
  
      // Store mat[i][1] in adj[(mat[i][0])] as mat[i][1] directs to mat[1][0]
      adj[(mat[i][0])].push_back(mat[i][1]);
      indeg[(mat[i][1])]++;
   }

   // Initialize a variable depth to store min different colors required
   int depth = 0;
   queue<int> q;
  
   for (int i = 1; i <= N; i++) {
      if (indeg[i] == 0) {
         q.push(i);
      }
   }
  
   if (q.empty())
      return 0;

   // Loop to use Topological sorting
   while (!q.empty()) {
      int size = q.size();
      for (int k = 0; k < size; k++) {
         int e = q.front();
         q.pop();
  
         for (auto it : adj[e]) {
            indeg[it]--;
            if (indeg[it] == 0) {
               q.push(it);
            }
         }
      }
      depth++;
   }
  
   // Return the minimum number of colours
   return depth;
}

// Driver code
int main(){
   int N = 5, M = 6;
   vector<int> mat[] = { { 1, 3 }, { 2, 3 }, { 3, 4 }, { 1, 4 }, { 2, 5 }, { 3, 5 } };

   // Function Call
   cout << min_colour(N, M, mat);
   return 0;
}

輸出

根據上述程式碼，輸出為：

3

輔助空間和時間複雜度均為：O(N + M)

圖著色的替代技術

讓我們看看一些解決頂點著色問題的方案。

  • 最簡單但效率最低的方法是蠻力搜尋。蠻力搜尋演算法包括嘗試所有可能的圖著色，並選擇顏色最少的那個。雖然這種方法保證找到最佳解決方案，但它的計算成本很高。此外，此方法僅適用於小型圖。

  • 第二種策略是區域性搜尋。區域性搜尋方法透過小的區域性調整迭代地改進現有答案。在頂點著色問題的情況下，區域性搜尋方法可以交換兩個相鄰頂點的顏色。它還可以嘗試只重新著色一個頂點。

  • 貪婪方法可用於解決頂點著色問題。這些演算法簡單有效。但是，它們並不總是產生最佳選擇。

  • 頂點著色問題也可以表示為整數線性規劃。這種方法可以找到問題的精確解。但是，對於大型圖，它可能會變得非常昂貴。

頂點著色的應用

  • 它在運籌學和計算機科學等各個領域都有多種用途。排程、路由、暫存器分配和無線頻率分配是一些最流行的頂點著色問題的應用。

  • 在排程問題中，我們必須將資源分配給可用的任務，同時避免衝突。為了解決這個問題，我們可以將每個任務表示為圖中的一個頂點，並將每個資源表示為一種顏色。此圖還允許我們計算色數。因此，色數表示執行所有任務而不發生衝突所需的最低資源數量。

  • 網路路由問題。資料包必須透過節點網路進行路由，而不會發生衝突。此外，我們可以使用頂點著色來描述這個問題，其中每個節點表示一個頂點，每條路徑表示圖中的顏色。

  • 編譯器必須使用計算機處理器中的暫存器為程式中的變數分配暫存器。我們可以使用頂點著色和色數原理來分配最少的暫存器來執行程式。

  • 在無線網路通訊中，頂點著色問題可用於將無線通道分配給裝置以減少干擾。

結論

在圖論中，頂點著色是圖示記的一個子集，它涉及將標籤傳遞給頂點或節點標籤以減少單個圖中使用的顏色數量。排程、路由、暫存器分配和無線頻率分配都是運籌學和計算機科學中頂點著色的應用。

更新於：2023年10月9日

瀏覽量161次

開啟你的職業生涯

完成課程後獲得認證

開始
廣告