資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
JavaScript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律使用 C++ 計算樹中兩個不相交路徑的最大乘積
在此問題中，我們提供一個具有 n 個節點的無根連通樹 T。我們的任務是編寫一個程式，使用 C++ 查詢樹中兩個不相交路徑的最大乘積。
問題說明 − 找到樹中兩個不相交路徑的最大乘積。我們將找到所有不相交的路徑，然後再計算其長度乘積。
我們舉個例子來說明這個問題，
輸入
圖形 −
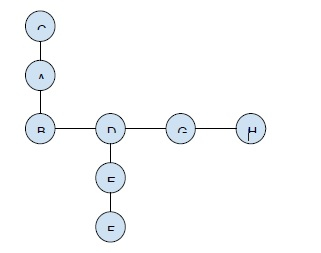
輸出
8
說明
考慮的不相交路徑是 C-A-B 和 F-E-D-G-H。
長度為 2 和 4。乘積 = 8。
解決方案
這個問題的解決方案是使用 DFS 遍歷樹。找到移除連線邊之後仍然唯一的路徑。然後，在路徑上進行迭代並找到其長度。然後，我們將兩條路徑配對並計算其長度的乘積。兩者被考慮的方式是使它們的乘積變為最大。
實現我們解決方案的程式，
範例
#include <bits/stdc++.h>
using namespace std;
int TreeTraverse(vector<int> graph[], int& currPathMax, int val1, int val2){
int max1 = 0, max2 = 0, maxVal = 0;
for (int i = 0; i < graph[val1].size(); i++) {
if (graph[val1][i] == val2)
continue;
maxVal = max(maxVal, TreeTraverse(graph, currPathMax,
graph[val1][i], val1));
if (currPathMax > max1) {
max2 = max1;
max1 = currPathMax;
}
else
max2 = max(max2, currPathMax);
}
maxVal = max(maxVal, max1 + max2);
currPathMax = max1 + 1;
return maxVal;
}
int FindMaxProductPath(vector<int> graph[], int Size) {
int maxProd = -10;
int pathA, pathB;
int currPathMax, prod;
for (int i = 0; i < Size; i++) {
for (int j = 0; j < graph[i].size(); j++){
currPathMax = 0;
pathA = TreeTraverse(graph, currPathMax, graph[i][j],i);
currPathMax = 0;
pathB = TreeTraverse(graph, currPathMax, i,graph[i][j]);
prod = (pathA * pathB);
maxProd = max(maxProd, prod);
}
}
return maxProd;
}
void insertEdge(vector<int> graph[], int val1, int val2){
graph[val1].push_back(val2);
graph[val2].push_back(val1);
}
int main(){
int Size = 8;
vector<int> graph[Size + 2];
insertEdge(graph, 1, 2);
insertEdge(graph, 2, 4);
insertEdge(graph, 3, 1);
insertEdge(graph, 5, 4);
insertEdge(graph, 7, 8);
insertEdge(graph, 8, 4);
insertEdge(graph, 5, 6);
cout<<"Maximum product of two non-intersecting paths of tree is "<<FindMaxProductPath(graph, Size)<<"\n";
return 0;
}輸出
Maximum product of two non-intersecting paths of tree is 8
更新於:2020 年 9 月 15 日
107 次瀏覽
廣告