資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟
心理學
社會科學
時裝研究
法律研究最大二分匹配
將圖中的一組邊選取出來，使得該組中的任意兩條邊不再同享一個端點。最大匹配是指匹配的邊數最多。
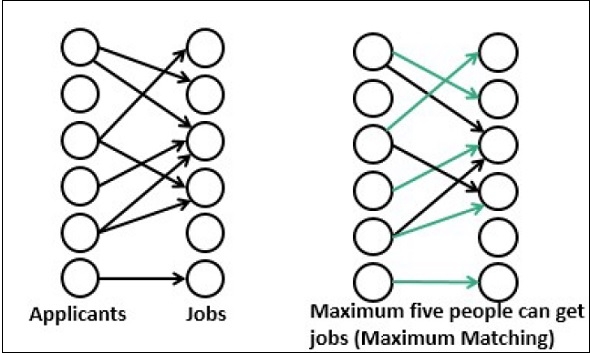
找到最大匹配後，我們無法再加入另一條邊。如果向最大匹配圖中新增一條邊，它將不再是一個匹配。對於二分圖，可能存在多於一個的最大匹配。
輸入和輸出
Input: The adjacency matrix. 0 1 1 0 0 0 1 0 0 1 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 Output: Maximum number of applicants matching for job: 5
演算法
bipartiteMatch(u, visited, assign)
輸入： 起始節點、用於跟蹤的已訪問列表、將列表分配給將節點分配給另一個節點。
輸出 − 在可以為頂點 u 匹配時返回 true。
Begin for all vertex v, which are adjacent with u, do if v is not visited, then mark v as visited if v is not assigned, or bipartiteMatch(assign[v], visited, assign) is true, then assign[v] := u return true done return false End
maxMatch(graph)
輸入 − 給定的圖。
輸出 − 匹配的最大數。
Begin initially no vertex is assigned count := 0 for all applicant u in M, do make all node as unvisited if bipartiteMatch(u, visited, assign), then increase count by 1 done End
示例
#include <iostream>
#define M 6
#define N 6
using namespace std;
bool bipartiteGraph[M][N] = { //A graph with M applicant and N jobs
{0, 1, 1, 0, 0, 0},
{1, 0, 0, 1, 0, 0},
{0, 0, 1, 0, 0, 0},
{0, 0, 1, 1, 0, 0},
{0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 1}
};
bool bipartiteMatch(int u, bool visited[], int assign[]) {
for (int v = 0; v < N; v++) { //for all jobs 0 to N-1
if (bipartiteGraph[u][v] && !visited[v]) { //when job v is not visited and u is interested
visited[v] = true; //mark as job v is visited
//when v is not assigned or previously assigned
if (assign[v] < 0 || bipartiteMatch(assign[v], visited, assign)) {
assign[v] = u; //assign job v to applicant u
return true;
}
}
}
return false;
}
int maxMatch() {
int assign[N]; //an array to track which job is assigned to which applicant
for(int i = 0; i<N; i++)
assign[i] = -1; //initially set all jobs are available
int jobCount = 0;
for (int u = 0; u < M; u++) { //for all applicants
bool visited[N];
for(int i = 0; i<N; i++)
visited[i] = false; //initially no jobs are visited
if (bipartiteMatch(u, visited, assign)) //when u get a job
jobCount++;
}
return jobCount;
}
int main() {
cout << "Maximum number of applicants matching for job: " << maxMatch();
}輸出
Maximum number of applicants matching for job: 5
更新於： 2020 年 6 月 16 日
8K+ 瀏覽量
廣告