線性規劃

---

簡介

線性規劃或線性最佳化是一種獨特的工具，用於獲得數學模型的最優（最大或最小）值。它縮寫為 LP，也稱為數學最佳化。在本教程中，我們將學習線性規劃、解決線性規劃問題的不同方法及其各種型別。

線性規劃

• 線性規劃被定義為數學最佳化過程，其中在特定約束條件下評估過程結果的最大值和最小值。

• 換句話說，它是一種最佳化線性目標函式的技術。

• 線性規劃問題 (LPP) 包括三個部分：目標函式、線性等式或約束以及非負限制。

• 目標函式是過程變數的線性函式，需要對其進行最佳化。

• 約束是過程變數的邊界限制或限制。線性規劃問題的標準形式可以表示為

目標函式 − $\mathrm{g(x_{1},x_{2}\:=\:q_{1}x_{1}\:+\:q_{2}x_{2})}$

約束 − $\mathrm{m_{11}x_{1}\:m_{12}x_{2}\:\leq\:s_{1}}$

$\mathrm{m_{21}x_{1}\:+\:m_{22}x_{2}\:\leq\:s_{2}}$

非負限制 − $\mathrm{x_{1}\:\geq\:0,\:x_{2}\:\geq\:0}$

解決 LPP 的方法

主要有兩種方法可以解決 LPP，例如

• 圖解法

• 單純形法

讓我們詳細討論每種方法。

圖解法

• 將 LPP 構造為標準形式。

• 在笛卡爾平面上繪製圖形並繪製約束線

• 確定每條約束線的有效側。

• 評估可行解區域並獲得角點

• 將角點代入目標函式以獲得所需結果

單純形法

• 步驟 1 − 第一步涉及將鬆弛變數新增到目標函式中，以將不等式轉換為方程形式。

• 步驟 2 − 構造初始單純形表並將目標函式寫為底行。

• 步驟 3 − 識別列中最負的條目並標記為樞軸列。

• 步驟 4 − 透過將最右列中的條目除以樞軸列中的條目來找到商。包含最小商的行標記為樞軸行。標記樞軸元素，即樞軸行和列的交點

• 步驟 5 − 透過執行基本運算使樞軸列的所有條目都變為零。

• 步驟 6 − 如果我們在底行得到非負整數，則停止此步驟；否則，從步驟 4 開始重複此步驟。

LPP 的型別

以下是下面討論的 LPP 型別。

營養

這種型別的 LPP 用於最佳化膳食計劃。換句話說，以最低預算最佳化食物攝入量是此 LPP 的目標。

• 目標函式 − 膳食預算

• 約束 − 食品中特定膳食的最低/最高量，例如糖和膽固醇。

生產/成本

這種型別的 LPP 涉及最佳化製造單位的淨利潤或生產率。

• 目標函式 − 生產率或淨利潤

• 約束 − 生產成本、員工成本、包裝成本等。

運輸

此 LPP 旨在以最低成本提供高效的運輸

• 目標函式 − 運輸成本

• 約束 − 商品的供應或需求

解題示例

示例 1

一種麵包需要 250 克麵粉和 20 克脂肪。另一種麵包需要 150 克麵粉和 30 克脂肪。求從 3 公斤麵粉和 0.6 公斤脂肪中可以生產的最大面包數量。

解決方案 −

步驟 1 − 讓我們將給定資料製成表格以便更好地理解

	麵粉重量（克）	脂肪重量（克）
第一種麵包 (x)	250	20
第二種麵包 (y)	150	30
可用量	3000	600

步驟 2 − 我們必須根據給定資料制定目標函式和約束條件。

目標函式 $\mathrm{g\:=\:x\:+\:y}$

約束 $\mathrm{250x\:+\:150y\:\leq\:3000\:or\:5x\:+\:3y\:\leq\:60}$

$\mathrm{20x\:+\:30y\:\leq\:600\:or\:2x\:+\:3y\:\:leq\:60}$

非負限制 $\mathrm{x_{1}\:\geq\:0\:,\:x_{2}\:\geq\:0}$

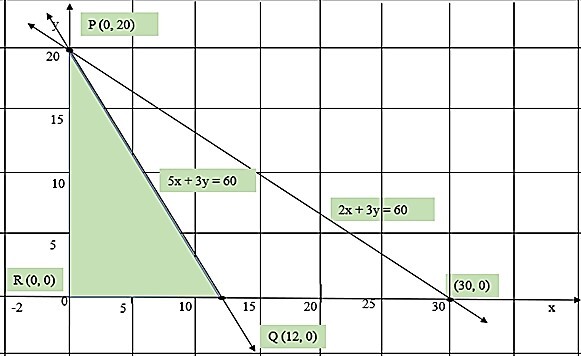
步驟 3 − 在笛卡爾平面上繪製直線，即 $\mathrm{5x\:+\:3y\:=\:60}$ 和 $\mathrm{2x\:+\:3y\:=\:60}$。

約束線 $\mathrm{5x\:+\:3y\:=\:60}$ 與座標軸在 (12, 0) 和 (0, 20) 處相交。因此，位於直線區域下方的任何點都滿足 $\mathrm{5x\:+\:3y\:\leq\:60}$

同樣，線 $\mathrm{2x\:+\:3y\:=\:60}$ 與座標軸在 (30, 0) 和 (0, 20) 處相交。因此，位於直線區域下方的任何點都滿足 $\mathrm{2x\:+\:3y\:\leq\:60}$。角點和目標函式的相應值如下所示

角點	$\mathrm{g(x,y)\:=\:x\:+\:y}$
P (0, 20)	20
Q (12. 0)	12
R (0,0)	0

∴可以形成的最大面包數量為 20，最優解為 (0,20)。

示例 2

使用單純形法求解 LPP。

最大化 $\mathrm{f(x,y)\:=\:7x\:+\:5y}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:x\:+\:2y\:\leq\:6}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:4x\:+\:3y\:\leq\:12}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:x,y\:\geq\:0}$

解決方案

將鬆弛變數新增到上述不等式中，將其轉換為方程

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:7x\:+\:5y\:=\:p}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:x\:+\:2y\:+\:q\:=\:6}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:4x\:+\:3y\:+\:r\:=\:12}$

單純形表如下所示。

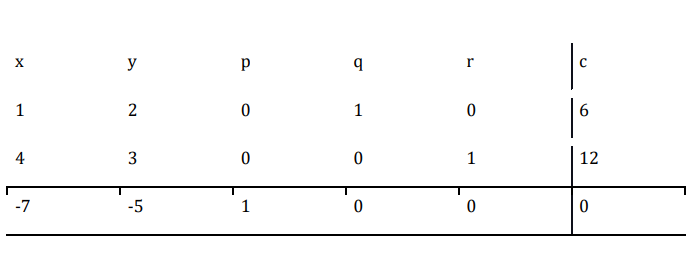
這裡，第一列是樞軸列，因為它包含最大的負數 $$

現在 $\mathrm{\frac{6}{1}\:=\:6\:and\:\frac{12}{4}\:=\:3}$

由於 3 是較小的商，因此第二行是樞軸行，答案 4 是樞軸元素。

現在，使用基本運算

$\mathrm{R_{2}\:\rightarrow\:\frac{R_{2}}{4}}$

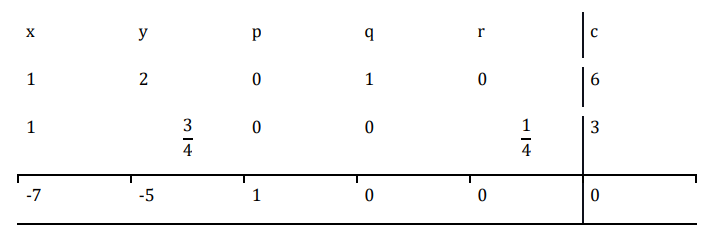
現在執行 $\mathrm{R_{1}\:\rightarrow\:R_{1}\:-\:R_{2}}$

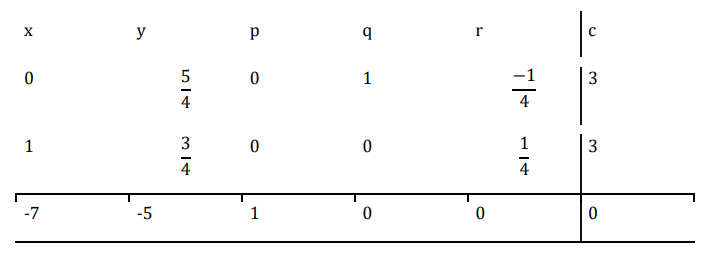
現在執行 $\mathrm{R_{3}\:\rightarrow\:7R_{2}\:+\:R_{3}}$

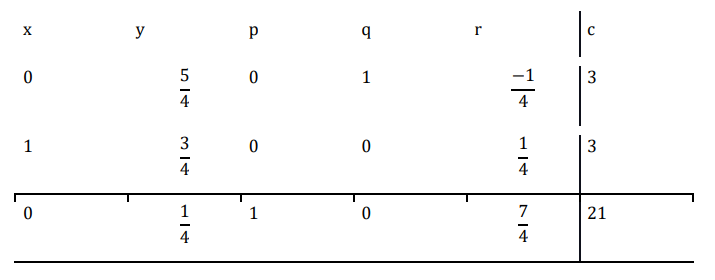
∴函式的最大值為 21，最優解為 (3,0)。

結論

本教程簡要介紹了線性規劃。此外，還簡要描述了各種型別和解決 LPP 的方法。此外，還提供了一些解題示例，以更好地闡明這一概念。總之，它可能有助於理解線性規劃問題的基本概念。

常見問題

1. 在圖解法中，您所說的可行區域是什麼意思？

可行區域是由滿足給定約束的座標界定的區域。

2. LP 的應用有哪些？

LP 有許多應用，包括生產排程、庫存策略、技術、倉庫建設等。

3. 定義目標函式？

目標函式是一個實值函式，需要對其進行最大化或最小化

4. 圖解法的侷限性是什麼？

隨著變數和約束的增加，圖解法變得複雜。它更適合於隨著變數和約束的增加而變得複雜的客觀函式。

5. LPP 可以有多個解嗎？

是的。LPP 可以有多個解。