資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學C++中最大的BST子樹
假設我們有一棵二叉樹；我們必須找到它最大的子樹，其中“最大”是指節點數最多的子樹。
因此，如果輸入類似於：
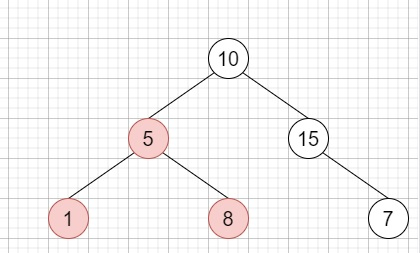
則輸出將為 3，因為在這種情況下，最大的 BST 子樹是突出顯示的那一個。
為了解決這個問題，我們將遵循以下步驟：
定義一個名為 data 的結構，其中包含四個值：size、maxVal、minVal 和 ok，ok 只能儲存 true/false 值
solve(TreeNode * node)
如果節點為空，則：
返回 Data，初始化為 (0, infinity, -infinity, true)
left := solve(node 的左子節點)
right := solve(node 的右子節點)
定義一個名為 curr 的 data
curr.ok := false
如果節點的值 >= right.minVal，則：
返回 curr
如果節點的值 <= left.maxVal，則：
返回 curr
如果 left.ok 為 true 且 right.ok 為 true，則：
curr.sz := 1 + left.sz + right.sz
curr.ok := true
curr.maxVal := (節點的值 和 right.maxVal) 的最大值
curr.minVal := (節點的值 和 left.minVal) 的最小值
如果 curr.ok 為 true，則：
ret := ret 和 curr.sz 的最大值
返回 curr
在主方法中，執行以下操作：
ret := 0
solve(root)
返回 ret
示例
讓我們看看以下實現以更好地理解：
#include <bits/stdc++.h>
using namespace std;
class TreeNode{
public:
int val;
TreeNode *left, *right;
TreeNode(int data){
val = data;
left = NULL;
right = NULL;
}
};
void insert(TreeNode **root, int val){
queue<TreeNode*> q;
q.push(*root);
while(q.size()){
TreeNode *temp = q.front();
q.pop();
if(!temp->left){
if(val != NULL)
temp->left = new TreeNode(val);
else
temp->left = new TreeNode(0);
return;
}
else{
q.push(temp->left);
}
if(!temp->right){
if(val != NULL)
temp->right = new TreeNode(val);
else
temp->right = new TreeNode(0);
return;
}
else{
q.push(temp->right);
}
}
}
TreeNode *make_tree(vector<int< v){
TreeNode *root = new TreeNode(v[0]);
for(int i = 1; i<v.size(); i++){
insert(&root, v[i]);
}
return root;
}
struct Data{
int sz;
int maxVal;
int minVal;
bool ok;
Data(){}
Data(int a, int b, int c, bool d){
sz = a;
minVal = b;
maxVal = c;
ok = d;
}
};
class Solution {
public:
int ret;
Data solve(TreeNode* node){
if (!node)
return Data(0, INT_MAX, INT_MIN, true);
Data left = solve(node->left);
Data right = solve(node->right);
Data curr;
curr.ok = false;
if (node->val >= right.minVal) {
return curr;
}
if (node->val <= left.maxVal) {
return curr;
}
if (left.ok && right.ok) {
curr.sz = 1 + left.sz + right.sz;
curr.ok = true;
curr.maxVal = max(node->val, right.maxVal);
curr.minVal = min(node->val, left.minVal);
}
if (curr.ok)
ret = max(ret, curr.sz);
return curr;
}
int largestBSTSubtree(TreeNode* root){
ret = 0;
solve(root);
return ret;
}
};
main(){
Solution ob;
vector<int< v = {10,5,15,1,8,NULL,7};
TreeNode *root= make_tree(v);
cout << (ob.largestBSTSubtree(root));
}輸入
[10,5,15,1,8,null,7]
輸出
3
更新於：2020年11月18日
101 次檢視
廣告