Lamport麵包店演算法

Lamport麵包店演算法是一種同步方法，用於解決平行計算系統中的臨界區問題。臨界區問題發生在多個程序同時需要訪問共享資源，但同一時間只有一個程序可以訪問的情況。挑戰在於確保每個程序以互斥的方式訪問資源，以避免衝突並保證系統的正確性。

Lamport麵包店演算法的虛擬碼

以下是Lamport麵包店演算法的虛擬碼：

  • 初始化一個大小為N的陣列choosing，其中N是程序的總數，所有元素都設定為0。

  • 初始化一個大小為N的陣列number，所有元素都設定為0。

  • 當每個程序i想要進入臨界區時，執行以下程式碼：

    • 設定choosing[i] = 1

    • 設定number[i] = max(number[0], number[1], ..., number[N-1]) + 1

    • 設定choosing[i] = 0

    • 對於其他每個程序j，重複執行以下操作，直到(number[j] == 0) 或 (number[i], i) < (number[j], j)：等待

    • 進入臨界區

  • 當每個程序i離開臨界區時，執行以下程式碼：

    • 設定number[i] = 0

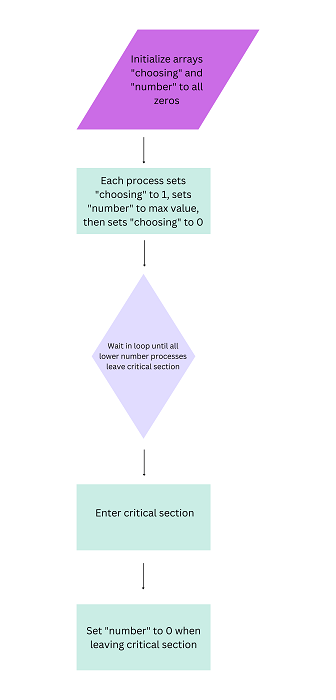
Lamport麵包店演算法的程式碼

以下程式碼演示了Lamport麵包店演算法的實際應用。本例中，我們將使用C++作為實現語言。

#include <iostream>
#include <atomic>
#include <thread>

#define N 5 
// total number of processes
using namespace std;

atomic<bool> entering[N] = {false}; 
// to keep track of which process is currently trying to enter critical section
atomic<int> number[N] = {0}; 
// to hold the ticket number for each process

void process(int i) {
   while (true) {
      // Step 1: Get ticket number
      entering[i] = true;
      int max_number = 0;
      for (int j = 0; j < N; j++) {
         if (number[j] > max_number) {
            max_number = number[j];
         }
      }
      number[i] = max_number + 1;
      entering[i] = false;

      // Step 2: Wait until it is this process's turn to enter the critical section
      for (int j = 0; j < N; j++) {
         while (entering[j]) {} 
         // wait until process j has finished choosing its ticket number
         while ((number[j] != 0) && ((number[j] < number[i]) || ((number[j] == number[i]) && j < i))) {} 
         // busy wait until it is this process's turn to enter the critical section
      }

      // Step 3: Enter the critical section
      cout << "Process " << i << " enters the critical section." << endl;
      // perform critical section operations here

      // Step 4: Exit the critical section
      number[i] = 0;
      cout << "Process " << i << " exits the critical section." << endl;
      // perform remainder section operations here
   }
}

int main() {
   // create threads for each process
   thread t[N];
   for (int i = 0; i < N; i++) {
      t[i] = thread(process, i);
   }

   // join threads
   for (int i = 0; i < N; i++) {
      t[i].join();
   }
   return 0;
}

輸出

Process 0 enters the critical section.
Process 0 exits the critical section.
Process 1 enters the critical section.
Process 1 exits the critical section.
Process 2 enters the critical section.
Process 2 exits the critical section.
Process 3 enters the critical section.
Process 3 exits the critical section.
Process 0 enters the critical section.
Process 0 exits the critical section.
Process 1 enters the critical section.
Process 1 exits the critical section.
Process 4 enters the critical section.
Process 4Process  exits the critical section.2
.............

Lamport麵包店演算法的優點

以下是Lamport麵包店演算法的優點：

  • 透過為請求訪問共享資源的程序或執行緒分配唯一的號碼，確保公平性。

  • 根據分配的號碼分配號碼，防止飢餓。

  • 基於號碼的策略簡單易懂，易於實現。

  • 高效，不需要複雜的資料結構或程序間通訊。

  • 提供互斥，無需專用硬體或硬體支援。

  • 廣泛適用且靈活，可應用於各種場景，以確保併發計算中的公平性和互斥。

  • 對於從事分散式或並行系統工作的軟體工程師來說，這是一個有用的工具。

Lamport麵包店演算法的缺點

  • 忙等待 - 該演算法需要忙等待，這可能會導致低效率和高CPU利用率，尤其是在許多程序或執行緒競爭訪問同一共享資源時。

  • 飢餓 - 雖然該演算法保證公平性，但沒有防止飢餓的保護措施。一個程序或執行緒有時可能會被無限期地延遲，從而無法獲得號碼並訪問資源。

  • 開銷 - 該演算法需要額外的記憶體和處理時間來確定號碼序列，因為它需要為每個程序或執行緒儲存狀態資訊。

  • 複雜性 - 該演算法的實現可能很複雜，因為它需要仔細處理競爭條件和死鎖，並且可能需要使用諸如互斥鎖或訊號量的同步機制。

結論

Lamport麵包店演算法是一種互斥演算法，它確保多個程序或執行緒可以訪問共享資源而不會相互干擾。它是一個簡單的演算法，可以防止飢餓並確保公平性。

該演算法透過為每個請求訪問資源的程序或執行緒分配號碼，然後比較這些號碼的值來確定它們被服務的順序。資源首先被分配給號碼最小的程序。

更新於：2023年5月3日

瀏覽量 1K+

開啟你的職業生涯

透過完成課程獲得認證

開始學習
廣告