NumPy 中的 Kaiser 窗 - Python

---

NumPy 中的 Kaiser 窗 – Python：簡介

Kaiser 窗是訊號處理和資料分析中一種典型的窗函式。它在頻譜分析、濾波器設計和加窗傅立葉變換等應用中發揮著重要作用。Kaiser 窗是一種流行的窗函式，在許多訊號處理和資料分析應用中至關重要。在任何應用中，包括頻譜分析、濾波器設計和加窗傅立葉變換，Kaiser 窗都提供了一種通用且適應性強的工具來管理主瓣寬度和旁瓣電平之間的權衡。

Kaiser 窗顯著減少了頻譜洩漏偽影和訊號洩漏，從而提高了資料分析方法的精度和可靠性。為了展示 Kaiser 窗在 Python 程式設計中的強大功能和適應性，本文將探討其概念、語法、在 NumPy 中的實現以及實際應用。

NumPy 中的 Kaiser 窗 - Python

Kaiser 窗的定義

Kaiser 窗，也稱為 Kaiser-Bessel 窗，是一種引數化的窗函式，可以管理主瓣寬度和旁瓣電平之間的權衡。它的目的是減少洩漏，洩漏發生在頻譜分析期間感興趣的訊號分散到相鄰頻率區間時。

語法

可以使用 NumPy 中的 numpy.kaiser 函式建立 Kaiser 窗，其語法如下：

numpy.kaiser(M, beta, sym=True)

其中，M 表示視窗長度，beta 決定其形狀，sym 指定視窗是否應是對稱的。

語法解釋

• 'M' − 視窗長度，通常為大於零的正整數。

• ‘beta’ − Kaiser 窗的形狀引數。它控制著旁瓣電平和主瓣寬度之間的權衡。較小的 beta 值會使主瓣變寬並增加旁瓣，而較大的 beta 值會導致主瓣變窄但旁瓣更高。通常，它是一個正實數。

• ‘sym’ − 一個可選引數，控制視窗是否應是對稱的。如果設定為 True，則生成的視窗將是對稱的。

演算法

• 步驟 1 − 匯入必要的庫

• 步驟 2 − 定義 Kaiser 窗的引數

• 步驟 3 − 使用 ‘numpy.kaiser’ 生成 Kaiser 窗

• 步驟 4 − 繪製 Kaiser 窗

• 步驟 5 − 檢查生成的視窗圖，以瞭解旁瓣電平和主瓣寬度如何相互影響。

方法

• 方法 1 − 用於頻譜分析的 Kaiser 窗

• 方法 2 − 用於濾波器設計的 Kaiser 窗

方法 1：用於頻譜分析的 Kaiser 窗

示例

import numpy as np
import matplotlib.pyplot as plt

# Generate a signal
N = 1024  # Number of samples
fs = 1000  # Sampling frequency
t = np.arange(N) / fs
f = 10  # Frequency of the signal
signal = np.sin(2 * np.pi * f * t)

# Apply the Kaiser window
window = np.kaiser(N, beta=10)
windowed_signal = signal * window

# Perform Fourier transform
spectrum = np.fft.fft(windowed_signal)
freq = np.fft.fftfreq(N, 1 / fs)

# Plot the spectrum
plt.plot(freq, np.abs(spectrum))
plt.title('Kaiser Window Spectrum Analysis')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude')
plt.grid(True)
plt.show()

輸出

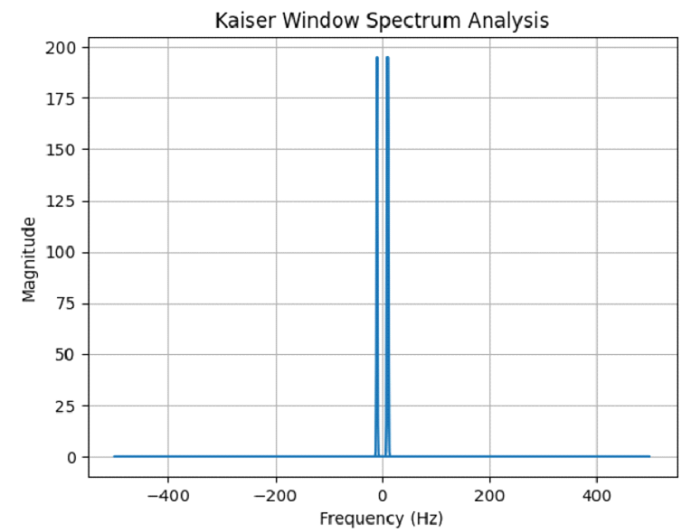
方法 1 的解釋

在這種方法中，我們使用 Kaiser 窗分析給定訊號的頻譜。我們將 Kaiser 窗應用於生成的正弦訊號。然後對加窗訊號應用傅立葉變換以獲得頻譜。透過檢視生成的頻譜圖，我們可以檢查訊號的頻譜特性，包括主瓣寬度和旁瓣電平。

應用 Kaiser 窗後，正弦訊號的頻譜圖將是提供的程式碼的輸出。圖表的縱軸顯示頻譜的幅度，而橫軸表示以 Hz 為單位的頻率。

生成的圖形將顯示主瓣寬度和旁瓣電平以及訊號的其他頻譜特性。Kaiser 窗的特性，如視窗長度和形狀引數 (beta)，將決定主瓣和旁瓣的確切形狀和分佈。

在處理訊號時，例如檢測主要頻率或濾除不需要的頻率，您可以透過分析圖表來識別訊號中存在的頻率成分及其幅度。

方法 2：用於濾波器設計的 Kaiser 窗

示例

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# Filter specifications
N = 101  # Filter order
fs = 1000  # Sampling frequency
fc = 100  # Cutoff frequency
taps = signal.firwin(N, fc, fs=fs, window=('kaiser', 8))

# Plot the filter coefficients
plt.stem(taps)
plt.title('Kaiser Window FIR Filter Coefficients')
plt.xlabel('Tap')
plt.ylabel('Magnitude')
plt.grid(True)
plt.show()

輸出

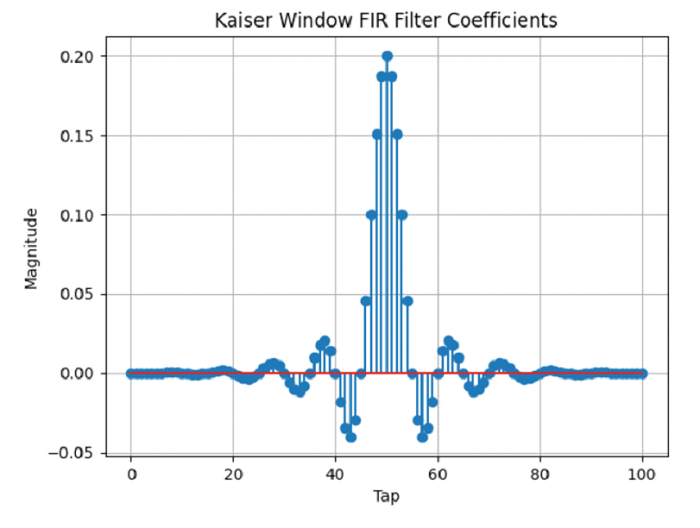
在此方法中，Kaiser 窗用於設計有限脈衝響應 (FIR) 濾波器。我們指定所需的截止頻率、取樣頻率和濾波器階數。將 Kaiser 窗應用於 scipy.signal.firwin 函式以生成濾波器係數。然後透過繪製生成的濾波器係數來顯示頻率響應特性。

使用 Kaiser 窗生成的 FIR 濾波器的濾波器係數的莖狀圖將是給定程式碼的輸出。圖表的橫軸顯示抽頭索引，而縱軸顯示濾波器係數的大小。

莖狀圖顯示了濾波器係數的幅度值，也顯示了濾波器的頻率響應特性。選擇的濾波器階數、截止頻率和應用於 Kaiser 窗的形狀引數 (beta) 將決定係數的確切形狀和值。

您可以透過檢查圖表來了解通帶特性、阻帶衰減和總體濾波器形狀，該圖表顯示了設計的濾波器的頻率響應。此資訊可用於訊號濾波、降噪和訊號重建等應用。

結論

Kaiser 窗是一種靈活的訊號處理和資料分析工具，可以控制主瓣寬度和旁瓣電平。本文介紹了 NumPy 中 Kaiser 窗的定義和語法。此外，我們還使用兩個實際方法演示了它在頻譜分析和濾波器設計中的應用。透過理解和有效地利用 Kaiser 窗，您可以改進您的 Python 訊號處理和分析任務。