Python中的Julia分形

---

Python中的Julia分形：介紹

分形是引人入勝的數學實體，展現出複雜且重複的圖案。Julia分形以法國數學家Gaston Julia的名字命名，是其中一個迷人的分形。透過對複數進行簡單的數學函式迭代，可以建立Julia分形。它一直是數學和計算機圖形學領域的研究和探索課題。本文將探索Julia分形的世界，並瞭解如何使用Python來生成它們。

Python中的Julia分形

定義

Julia分形的公式是一個複雜的迭代函式。它是透過在複平面上對每個點重複求解以下方程得到的：

Z_{n+1} = Z_{n}^2 + C

其中，“Z_n”表示第n次迭代時的複數，“Z_n+1”表示第(n+1)次迭代時的複數，“C”是一個固定的複數，它決定了分形的結構。生成的圖案是透過根據每個點達到給定幅度閾值所需的迭代次數對其進行顏色編碼來建立的。不同的顏色用於區分逃逸到無窮大和限制在一定範圍內的點。

演算法

• 步驟1 - 定義最終影像的寬度和高度。

• 步驟2 - 透過更改縮放級別、x和y偏移量來更改分形的位置和放大倍數。

• 步驟3 - 指定逃逸閾值和最大迭代次數。

• 步驟4 - 使用指定的引數呼叫'julia_fractal()'函式。

• 步驟5 - 使用命令'plt.show()'顯示生成的Julia分形。

方法

• 方法1 - 使用matplotlib庫生成曼德勃羅集的影像。

• 方法2 - 使用matplotlib庫和正弦函式生成曼德勃羅集的影像。

方法1：使用matplotlib庫生成曼德勃羅集的影像

示例

import numpy as np
from matplotlib import pyplot as plt
image_x = 400
image_y = 300
mesh_x = np.linspace(-2.5,1.5, num= image_x + 1)
mesh_y = np.linspace(-1.5,1.5, num= image_y + 1)
image = np.zeros((len(mesh_y), len(mesh_x)))
for i,y in enumerate(mesh_y):
   for j, x in enumerate(mesh_x):
      cr, ci = x,y
	  zr, zi = 0,0 
	  count = 0
	  color = ‘black’
	  while count<= 50:
	     count = count + 1
		 z_mod_sq = zr*zr + zi*zi
		 if z_mod_sq > 4:
		    color = ‘white’
			break
		 #zr + I zi = zr^2 – zi^2=2zrziI+ cr +I ci
		 zr, zi = (zr*zr – zi*zi + cr), (2*zr*zi + ci)
	   if color != ‘white’:
	      image[i][j] = 1
	   else:
	      image[i][j] = count
plt.imshow(image)
plt.show()

輸出

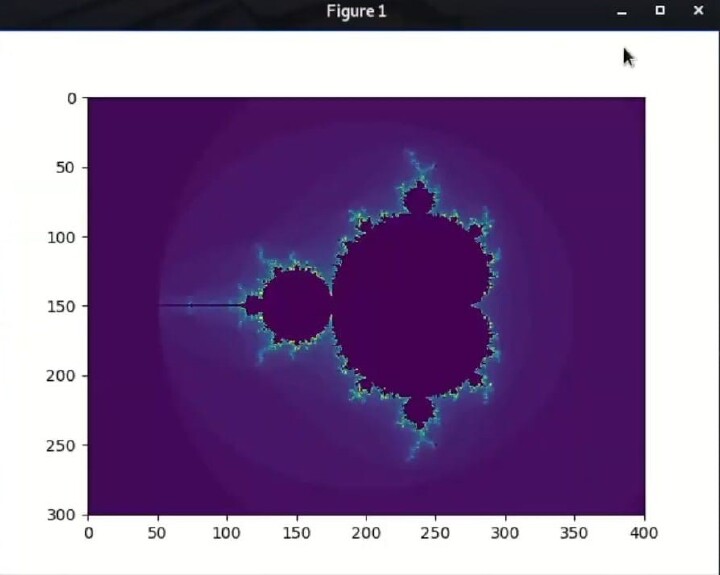
程式碼實現了著名的數學分形——曼德勃羅集。曼德勃羅集是透過對複數迭代應用函式，並確定結果是否逃逸到無窮大或保持有界來生成的。此程式碼中，複平面上每個畫素都由一個複數表示。對於每個畫素，演算法都確定迭代函式在預定次數的迭代內（本例中為50次）是否會逃逸到無窮大。如果函式逃逸到無窮大，則相應的畫素被著色為白色；否則，被著色為黑色。輸出顯示了曼德勃羅集的複雜且重複的圖案。

方法2：使用matplotlib庫和正弦函式生成曼德勃羅集的影像

示例

import numpy as np
from matplotlib import pyplot as plt
image_x = 400
image_y = 300
mesh_x = np.linspace(-2.5,1.5, num= image_x + 1)
mesh_y = np.linspace(-1.5,1.5, num= image_y + 1)
image = np.zeros((len(mesh_y), len(mesh_x)))
for i,y in enumerate(mesh_y):
   for j, x in enumerate(mesh_x):
      cr, ci = x,y
	  zr, zi = 0,0 
	  count = 0
	  color = 'black'
	  while count<= 50:
         count = count + 1
		 z_mod_sq = zr*zr + zi*zi
		 if z_mod_sq > 4:
		    color = 'white'
			break
		 #zr + I zi = zr^2 – zi^2=2zrziI+ cr +I ci
		 zr, zi = (zr*zr – zi*zi + cr), (2*zr*zi + ci)
	  if color != ‘white’:
	     image[i][j] = 1
      else:
	     import math
		 image[i][j] = int(math.sin(count) * 10)
plt.imshow(image)
plt.show()

輸出

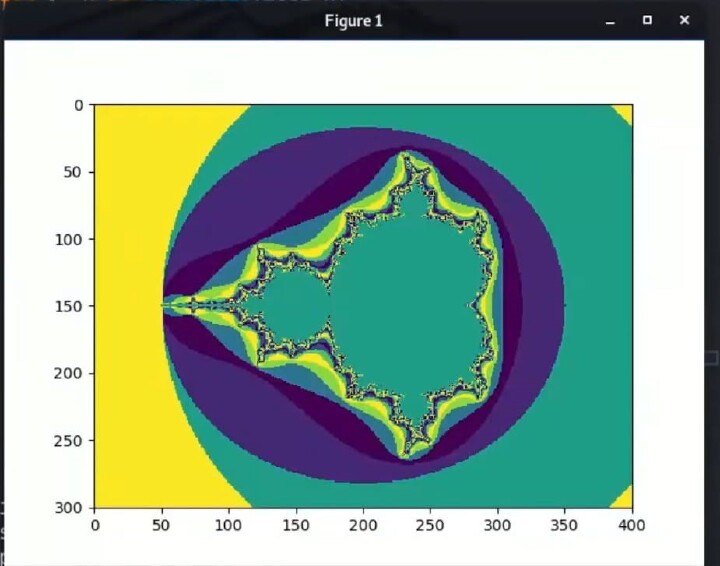
程式碼仍然實現了曼德勃羅集，但對未逃逸到無窮大的畫素的顏色分配做了一點修改。修改後的程式碼根據迭代計數的值為這些畫素分配不同的灰色陰影，而不是使用二進位制的黑白顏色方案。迭代計數的值乘以10，然後透過正弦函式傳遞，以生成一系列灰色值。這將曼德勃羅集轉換為視覺上令人愉悅的灰度表示形式，突出了分形的精細特徵。

現在，修改後的程式碼根據迭代次數為畫素分配灰度值，從而使影像具有漸變的外觀。重寫的程式碼使用正弦函式將迭代計數轉換為-1到1之間的值，而不是簡單地使用二進位制的黑白顏色。此值乘以10並轉換為整數後，會生成一系列灰色顏色。此更新旨在透過視覺方式突出顯示與曼德勃羅集的不同程度的偏差，從而生成更細緻和美觀的影像。

結論

Julia分形為我們提供了一個迷人的視窗，可以窺探數學的無限複雜性和精緻之美。在本教程中，我們探討了Julia分形的概念，並學習瞭如何使用Python來生成它們。我們定義了Julia分形函式，解釋了其語法，並提供了生成Julia分形的逐步演算法。此外，我們提供了兩種不同的方法，並附帶可執行程式碼和結果。透過調整不同的引數，包括縮放、偏移量、最大迭代次數、逃逸閾值和常數值，可以生成各種引人入勝的Julia分形圖案。互動式方法允許即時探索，從而促進對底層數學概念和Julia分形的獨特特性的更深入理解。

Python憑藉其豐富的科學庫（包括NumPy和Matplotlib），為生成和顯示分形提供了強大的環境。因此，請深入探索Julia分形的世界，盡情發揮你的想象力，踏上探索分形幾何無限壯麗的永恆之旅。