資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會科學
時裝研究
法律研究C++ 中的線索二叉樹的中序遍歷
這裡我們將瞭解線索二叉樹資料結構。我們知道二叉樹節點最多有兩個子節點。但如果它們只有一個子節點或沒有子節點，那麼在連結串列表示中，連結部分將保持為 null。使用線索二叉樹表示時，我們可以透過建立一些執行緒來重用這些空連結。
如果某個節點有一些空閒的左或右子節點區域，那將用作執行緒。線索二叉樹有兩種型別：單線索樹或全線索二叉樹。
對於全線索二叉樹，每個節點都有五個欄位。三個欄位與正常二叉樹節點類似，另外兩個欄位用於儲存布林值，以表示該側的連結是實際連結還是執行緒。
| 左執行緒標誌 | 左連結 | 資料 | 右連結 | 右執行緒標誌 |
這是全線索二叉樹
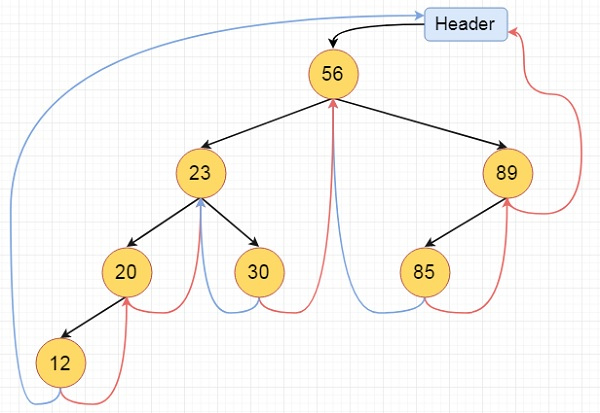
演算法
inorder(): Begin temp := root repeat infinitely, do p := temp temp = right of temp if right flag of p is false, then while left flag of temp is not null, do temp := left of temp done end if if temp and root are same, then break end if print key of temp done End
示例
#include <iostream>
#define MAX_VALUE 65536
using namespace std;
class N { //node declaration
public:
int k;
N *l, *r;
bool leftTh, rightTh;
};
class ThreadedBinaryTree {
private:
N *root;
public:
ThreadedBinaryTree() { //constructor to initialize the variables
root= new N();
root->r= root->l= root;
root->leftTh = true;
root->k = MAX_VALUE;
}
void insert(int key) {
N *p = root;
for (;;) {
if (p->k< key) { //move to right thread
if (p->rightTh)
break;
p = p->r;
}
else if (p->k > key) { // move to left thread
if (p->leftTh)
break;
p = p->l;
}
else {
return;
}
}
N *temp = new N();
temp->k = key;
temp->rightTh= temp->leftTh= true;
if (p->k < key) {
temp->r = p->r;
temp->l= p;
p->r = temp;
p->rightTh= false;
}
else {
temp->r = p;
temp->l = p->l;
p->l = temp;
p->leftTh = false;
}
}
void inorder() { //print the tree
N *temp = root, *p;
for (;;) {
p = temp;
temp = temp->r;
if (!p->rightTh) {
while (!temp->leftTh) {
temp = temp->l;
}
}
if (temp == root)
break;
cout<<temp->k<<" ";
}
cout<<endl;
}
};
int main() {
ThreadedBinaryTree tbt;
cout<<"Threaded Binary Tree\n";
tbt.insert(56);
tbt.insert(23);
tbt.insert(89);
tbt.insert(85);
tbt.insert(20);
tbt.insert(30);
tbt.insert(12);
tbt.inorder();
cout<<"\n";
}輸出
Threaded Binary Tree 12 20 23 30 56 85 89
更新於：10-8-2020
4K+ 瀏覽量
廣告