資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法學資料結構中的高度偏左樹
在這裡，我們將瞭解什麼是高度平衡左傾樹 (HBLT)。考慮一個二叉樹，其中一個特殊的節點，稱為**外部節點**，替換每個空子樹。所有其他節點稱為**內部節點**。當一些外部節點新增到某個二叉樹中時，這稱為**擴充套件二叉樹**。
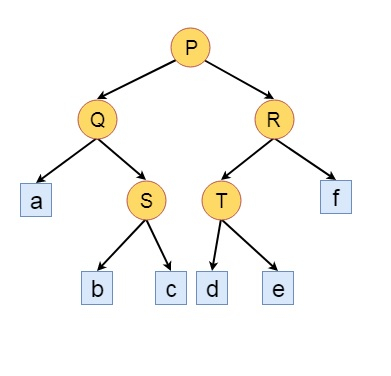
如果我們不考慮這棵樹的葉子邊，那麼那就是實際的二叉樹，而這是擴充套件的二叉樹。
現在假設*s(x)*是從節點x到其子樹中外部節點的最短路徑的長度。如果x是外部節點，則其*s(x)*值為0。如果x是內部節點，則其值為：
min{𝑠(𝐿), 𝑠(𝑅)} + 1這裡L和R分別是x的左孩子和右孩子。現在讓我們看看給定樹的s值。
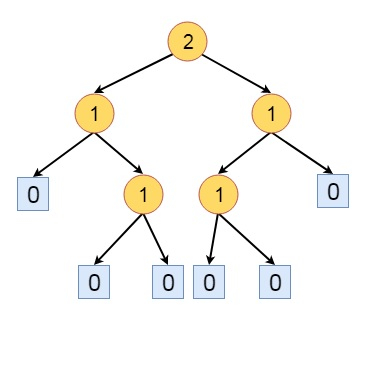
HBLT的定義如下：當且僅當每個內部節點的左孩子的s值大於或等於右孩子的s值時，二叉樹才是高度平衡左傾樹(HBLT)。
上圖中的樹不是HBLT。節點a的父節點具有s(L) = 0，而s(R)為1，除了所有其他節點都滿足HBLT的規則。因此，如果我們調整該節點的左子樹和右子樹，使其成為HBLT。
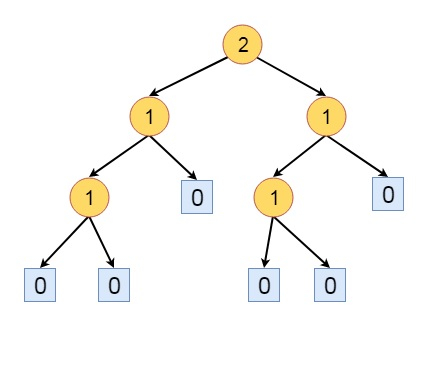
其他一些定義是：
最大樹（最小樹）是一棵樹，其中每個節點的值都大於（小於）或等於其子節點。
最大HBLT是一個也是最大樹的HBLT，最小HBLT是一個也是最小樹的HBLT。
更新於：2020年8月11日
1K+ 次瀏覽
廣告