資料結構中的赫夫曼樹
定義
赫夫曼編碼為字元提供程式碼,程式碼長度取決於相應字元的相對頻率或權重。赫夫曼編碼採用可變長度,且無任何字首(即任何程式碼都不是其他程式碼的字首)。任何無字首的二進位制程式碼都可以表示為二叉樹,其中編碼的字元儲存在葉節點。
赫夫曼樹或赫夫曼編碼樹定義為一棵滿二叉樹,其中樹的每個葉節點對應於給定字母表中的一個字母。
赫夫曼樹被視為具有最小外部路徑權重的二叉樹,即它與給定葉節點集的加權路徑長度總和最小。因此,目標是構建一棵具有最小外部路徑權重的樹。
舉例說明:
字母頻率表
| 字母 | z | k | m | c | u | d | l | e |
| 頻率 | 2 | 7 | 24 | 32 | 37 | 42 | 42 | 120 |
赫夫曼編碼
| 字母 | 頻率 | 程式碼 | 位元 |
|---|---|---|---|
| e | 120 | 0 | 1 |
| d | 42 | 101 | 3 |
| l | 42 | 110 | 3 |
| u | 37 | 100 | 3 |
| c | 32 | 1110 | 4 |
| m | 24 | 11111 | 5 |
| k | 7 | 111101 | 6 |
| z | 2 | 111100 | 6 |
霍夫曼樹(對於上述示例)如下所述 -
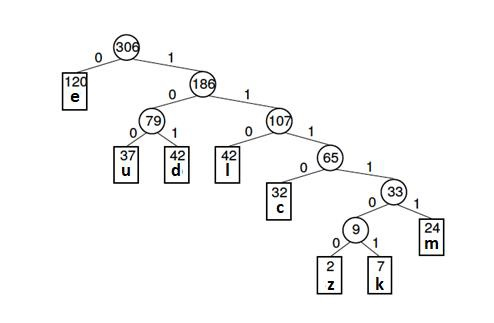

廣告

 資料結構
資料結構 網路
網路 RDBMS
RDBMS 作業系統
作業系統 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 程式設計
C 程式設計 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP