資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究DEPQ 的通用方法
雙堆
存在從單端優先佇列 (PQ) 資料結構推匯出高效 DEPQ（雙端優先佇列）資料結構的通用方法，這些方法也提供了 remove(aNode) 操作的高效實現（此操作從 PQ 中消除節點 aNode）。最簡單的方法，即雙結構方法，同時跟蹤所有 DEPQ 元素的最小 PQ 和最大 PQ，並在最小 PQ 和最大 PQ 的節點之間保持對應指標，這些節點包含相同的元素。
圖 A 顯示了元素 7、8、3、6、5 的雙堆結構。對應指標顯示為紅色箭頭。
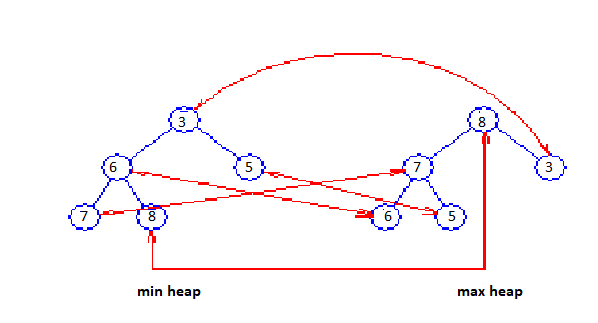
圖 A：雙堆
雖然圖中顯示每個元素都儲存在最小堆和最大堆中，但實際上只需要在兩個堆中的一箇中儲存每個元素。
isEmpty 和 size 操作是透過實現一個跟蹤 DEPQ 中元素數量的變數 size 來實現的。最小元素位於最小堆的根部，最大元素位於最大堆的根部。要插入元素 A，我們將 A 插入到最小堆和最大堆中，然後在 A 在最小堆和最大堆中的位置之間設定對應指標。要消除最小元素，我們從最小堆中執行 removeMin，並從最大堆中執行 remove(aNode)，其中 aNode 是已移除元素的對應節點。最大元素的消除方式類似。
總對應和葉對應
總對應和葉對應是更復雜的對應技術。在這兩種技術中，一半的元素位於最小 PQ 中，另一半位於最大 PQ 中。當元素數量為奇數時，一個元素儲存在緩衝區中。此緩衝區元素不屬於任何 PQ。在總對應技術中，最小 PQ 中的每個元素 x 都與最大 PQ 的不同元素 y 配對。(x, y) 是一個對應的元素對，使得 priority(x) <= priority(y)。
圖 B 顯示了 11 個元素 3、4、5、5、6、6、7、8、9、10、11 的總對應堆。元素 10 位於緩衝區中。對應對由紅色箭頭顯示。
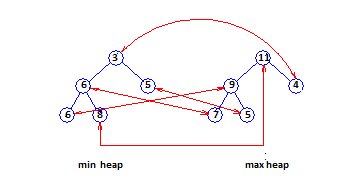
圖 B：總對應堆
在葉對應技術中，最小和最大 PQ 的每個葉元素都需要成為對應對的一部分。非葉元素不需要在任何對應對中。圖 C 顯示了一個葉對應堆。
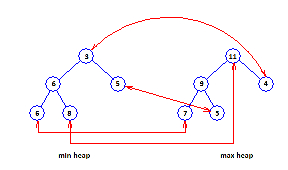
圖 C：葉對應堆
總對應和葉對應結構比雙結構需要更少的空間。但是，總對應和葉對應結構的 DEPQ 演算法比雙結構的演算法更復雜。在三種對應技術中，葉對應是速度最快的 DEPQ 對應結構。
透過實現任何描述的對應技術，我們可以從堆、高度偏差左傾樹和配對堆中得到 DEPQ 結構。在這些 DEQP 結構中，put(x)、removeMin() 和 removeMax() 操作消耗 O(log n) 時間（n 是 DEPQ 中的元素數量，對於配對堆，這是攤銷複雜度），其餘 DEPQ 操作消耗 O(1) 時間。
瀏覽量：112
