解釋用於檢查有損或無損分解的演算法

如果無法在不丟失資訊的情況下從分解後的表中重建原始表，則稱分解為**有損**。

如果可以使用自然連線在不丟失任何資訊的情況下重建原始表，則稱分解為**無損**。

演算法

下面是用於檢查分解是有損還是無損的演算法：

• **步驟 1** - 建立一個包含 M 行 N 列的表

  • M = 分解關係的數量。

  • N = 原始關係的屬性數量。

• **步驟 2** - 如果分解關係 Ri 包含屬性 A，則

• 在位置 (Ri,A) 插入一個符號（例如 'a'）。

• **步驟 3** - 考慮每個 FD X->Y

  • 如果列 X 包含兩個或多個符號，則

    在列 Y 的相同位置（行）插入符號。

• **步驟 4** - 如果任何一行完全填充了符號，則

  • 分解是無損的。

  • 否則

    • 分解是有損的。

問題

考慮一個示例，以檢查給定的關係是否可以透過應用上述演算法進行有損或無損分解。

考慮 R(A,B,C,D,E)

F:{A->B, BC->E, ED->A}

R 分解為 R1(AB) 和 R2(ACDE)。檢查分解是有損還是無損。

解決方案

按照以下步驟確定給定的分解是無損還是有損：

步驟 1

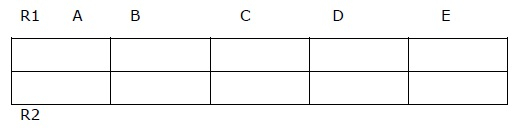
步驟 2

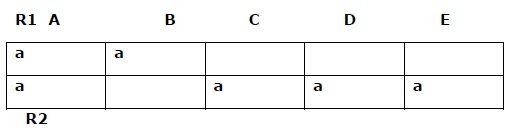
步驟 3

現在讓我們在第二列第二行中為 A->B 插入符號 'a'

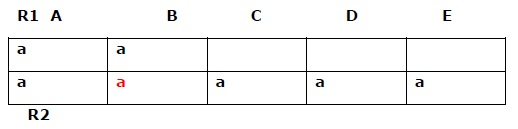
R2 完全填充 => 分解是無損的。

Bhanu Priya

更新於: 2021-07-03

3K+ 次檢視

開啟你的 職業生涯

透過完成課程獲得認證

開始學習