點電荷的電勢

---

介紹

很多人對“電勢”這個術語感到非常困惑。在我們上學的時候，第一次聽到這個詞的時候，我們瞭解到電勢與位置有一定的關係。然而，它指的是容量或強度。電勢這個術語代表了電的強度。

當我們開始學習電學時，首先要面對的就是電荷。電荷是電子學的基石。它分為兩種型別：正電荷和負電荷。隨著我們對電荷的深入瞭解，我們開始認識到電場、電勢、電勢能、偶極子等概念。每一個單獨的電荷或電荷的聚集體都有其影響範圍，在這個範圍內，我們可以體驗到吸引力和排斥力，或者在該區域的每個位置產生電勢。

什麼是電勢？

簡單來說，我們可以說，在一個存在有效電場的區域中，某一點的電勢是指我們將一個大小為1庫侖的正點電荷從無限遠處移動到我們所考慮的該點（該點受到持續存在的靜電力影響）所需要做的功。

因此，電勢也可以表示為作用在單位電荷上的功。伏特是電勢的標準測量單位。因此，一個1伏特的電勢點是指將一個位於無限遠處的正點電荷移動到目標點所需要做的1焦耳的功。整個過程也受到電場產生的力的影響。

$$\mathrm{V=\frac{W}{q}}$$

點電荷產生的電勢

我們都知道，每個電荷和多個電荷的組合都有其影響範圍，稱為電場。在該電場中，我們可以感受到一些靜電力。點電荷也會產生電勢。在下面的部分中，我們將研究點電荷產生的電勢。

點電荷在檢驗電荷處產生的電勢

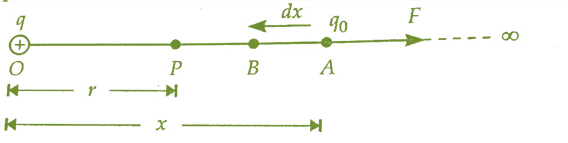
這裡，一個正電荷q位於點O。現在，我們將計算距離O點r距離處的點P處的電勢。根據定義，電勢等於我們將一個單位正電荷從無限遠處移動到我們所考慮的點P所做的功。

現在，假設在A點，距離O點x距離處有一個檢驗電荷$\mathrm{q_{0}}$。

利用庫侖定律，我們可以計算出檢驗電荷由於q電荷而受到的力，

$$\mathrm{F=\frac{1}{4\pi \epsilon _{0}}.\frac{qq_{0}}{x^{2}}}$$

由於電場產生的力F的方向與$\mathrm{q_{0}}$電荷從A點移動到B點的方向相反，因此我們必須對電荷做少量功，才能使其克服q電荷產生的力，並使其發生dx位移。

因此，

$$\mathrm{dW=\overrightarrow{F}.\overrightarrow{dx}=F.dxcos\:180^{\circ}}$$

$$\mathrm{dW=-F\:dx}$$

dW 是少量功。

檢驗電荷從任何無限遠處移動到點P所需的總功可以透過積分計算得出

$$\mathrm{W=\int dW=-\int_{\infty }^{r}F\:dx}$$

$$\mathrm{W=-\int_{\infty }^{r}\frac{1}{4\pi \epsilon _{0}}.\frac{qq_{0}}{x^{2}}\:dx}$$

$$\mathrm{W=-\frac{qq_{0}}{4\pi \epsilon _{0}}\int_{\infty }^{r}x^{-2}\:dx}$$

$$\mathrm{W=-\frac{qq_{0}}{4\pi \epsilon _{0}}\left [ -\frac{1}{x} \right ]_{\infty }^{r}}$$

$$\mathrm{W=\frac{qq_{0}}{4\pi \epsilon _{0}}\left [ \frac{1}{r}-\frac{1}{\infty } \right ]}$$

$$\mathrm{W=\frac{1}{4\pi \epsilon _{0}}.\frac{qq_{0}}{r}}$$

因此，從上述表示式可以看出，將檢驗電荷從無限遠處移動到點P所需的功為

$$\mathrm{W=\frac{1}{4\pi \epsilon _{0}}.\frac{qq_{0}}{r}}$$

現在，我們知道電勢為

$$\mathrm{V=\frac{W}{q_{0}}}$$

因此，

$$\mathrm{V=\frac{1}{4\pi \epsilon _{0}}.\frac{q}{r}}$$

多個電荷產生的電勢

在這裡，我們將測量由於N個電荷組成的系統在任意一點處的電勢。假設系統中存在N個點電荷，即$\mathrm{q_{1},q_{2},q_{3},q_{4},q_{5},q_{6},q_{7}.....q_{N}}$。所有點電荷距離我們所考慮的點P的距離分別為$\mathrm{r_{1},r_{2},r_{3},r_{4},r_{5},r_{6},r_{7}.....r_{N}}$。

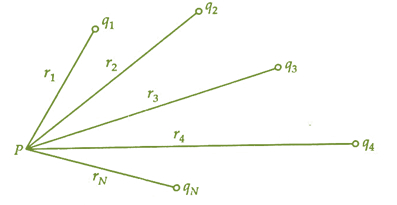
從上一節我們知道，點電荷在任意點P處的電勢為

$$\mathrm{V=\frac{1}{4\pi \epsilon _{0}}.\frac{q}{r}}$$

對於電荷$\mathrm{q_{1}}$

$$\mathrm{V_{1}=\frac{1}{4\pi \epsilon _{0}}.\frac{q_{1}}{r_{1}}}$$

同樣，對於其他$\mathrm{q_{1},q_{2},q_{3},q_{4},q_{5},q_{6},q_{7}.....q_{N}}$，我們得到

$$\mathrm{V_{1}=\frac{1}{4\pi \epsilon _{0}}.\frac{q_{1}}{r_{1}},V_{2}=\frac{1}{4\pi \epsilon _{0}}.\frac{q_{2}}{r_{2}},V_{3}=\frac{1}{4\pi \epsilon _{0}}.\frac{q_{3}}{r_{3}}............V_{N}=\frac{1}{4\pi \epsilon _{0}}.\frac{q_{N}}{r_{N}}}$$

我們還知道，電勢不是向量，而是標量，因此，計算N個電荷在任意點P處的總電勢將是每個電荷的個體電勢的總和。

因此，

$$\mathrm{V=V_{1},V_{2},V_{3},V_{4}+........+V_{N}}$$

$$\mathrm{V=\frac{1}{4\pi \epsilon _{0}}.\frac{q_{1}}{r_{1}}+\frac{1}{4\pi \epsilon _{0}}.\frac{q_{2}}{r_{2}}+\frac{1}{4\pi \epsilon _{0}}.\frac{q_{3}}{r_{3}}............+\frac{1}{4\pi \epsilon _{0}}.\frac{q_{N}}{r_{N}}}$$

$$\mathrm{V=\frac{1}{4\pi \epsilon _{0}}\left [ \frac{q_{1}}{r_{1}}+ \frac{q_{2}}{r_{2}}+\frac{q_{3}}{r_{3}}+......+\frac{q_{N}}{r_{N}}\right ]}$$

我們也可以用求和的形式寫出上述方程，

$$\mathrm{V=\frac{1}{4\pi \epsilon _{0}}\sum_{i=1}^{N}\frac{q_{i}}{r_{i}}}$$

這是N個電荷系統中任意點（此處用P表示）處的總電勢。

結論

在以上各節中，我們研究了單個電荷和多個電荷在任意點處的電勢。我們注意到，電勢是由電荷的球對稱性引起的。此外，電勢是標量，因此對於多個電荷，我們可以透過簡單的加法計算它。

常見問題

Q1. 在任何一點，我們是否可以發現電勢為零，但該點的電場不為零？

A1. 是的，我們可以找到這樣的情況。我們知道，偶極子軸線上垂直方向的赤道點處的電勢為零，但當我們在該點測試電場時，我們會感受到一些電場的影響。

Q2. 如果我們沿著電場線移動，電勢會發生什麼變化？

A2. 在這種情況下，我們會發現電勢沿電場線方向減小。

Q3. 電勢的標準單位的基本單位形式是什麼？

A3. 電勢標準單位的基本單位形式為

$$\mathrm{Potential=\frac{Work\:done}{charge}}$$

因此，

$$\mathrm{\frac{ML^{2}T^{-2}}{AT}=ML^{2}T^{-3}A^{-1}}$$

Q4. 為什麼導體內部的電勢是恆定的？

A4. 我們知道，電勢與電場存在直接關係。任何導體內部的電場都為零，因此導體內的電勢是恆定的。我們可以用以下表達式證明這一點，

$$\mathrm{E=-\frac{dV}{dr}}$$

當E = 0時

$$\mathrm{\frac{dV}{dr}=0}$$

$$\mathrm{V= Constant}$$

Q5. 等勢面是什麼意思？

A5. 等勢面是指整個表面上每一點的電勢都相等的表面。