動力學與運動學的區別

---

介紹

許多學生在學習或討論動力學和運動學時都會犯錯誤。事實上，由於發音相似，學生們常常將這兩個術語混為一談，但這是不正確的。動力學和運動學是不同的，用於不同的目的。簡單來說，動力學可以定義為處理物體運動的物理學分支。而運動學則是另一個處理速度、加速度等大小的體系。兩者都是物理學的分支。

什麼是動力學？

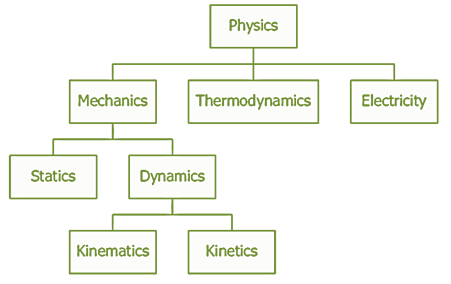
動力學是力學的另一個名稱，它是物理學的一個分支。這個物理學分支處理物體的運動。在這個分支中，我們研究所有運動的原因以及由於施加力而導致的物體變化。

歷史上這些術語的出現是因為我們看到，每當物體運動時，肯定有一些力或力矩在背後推動這個運動，所以要研究這個力矩或力，我們就必須處理動力學。物體由於任何外加力的各種運動都在動力學的規則下進行研究。在這個分支中，我們處理一些與物體運動相關的量，例如力、力矩等。動力學是研究力原因的完全理論或概念性物理學領域。

動力學的例子

• 水力發電完全基於動力學的原理。

• 風車是由於動力學現象而工作的。

• 我們的汽車和腳踏車

• 從發射器發射導彈

動力學的重要性

動力學對地球上和太空中的每個人都非常重要。今天，我們在工程方面非常先進，但誰會忘記，實際上，所有機器都在動力學的原理上工作。從最小到最大的每一次創新都或多或少地應用了動力學物理學。在我們的日常生活中，我們使用的風扇、空調、車輛等都是由於力的作用而工作的。

動力學的一些關鍵重要性如下所示。

• 交通運輸：由於動力學，所有車輛都能夠藉助發動機產生的足夠扭矩來實現平穩運動，這有助於所有公共汽車、汽車、卡車等的移動。

• 能源生產：電力生產完全基於渦輪機的旋轉，而渦輪機的工作原理是動力學。在水力發電廠中，當具有高動能的水從高海拔流向低海拔時，會使渦輪機旋轉併發電。

• 藥物的化學反應：在醫學科學領域，動力學起著至關重要的作用。在藥物發明中，我們根據其動力學特性（如它們如何反應，為什麼它們促進反應等）對化合物進行分析。

• 空間火箭推進：利用所有動力學定律，我們找到最佳的航天器軌跡，以最低的成本安全地到達目的地。

• 藥物注射：當我們注射合適的藥物到體內進行治療時，藥物顆粒的運動遵循動力學原理，我們還在裝置中使用合適的壓力以正確的方式進行注射。

什麼是運動學？

運動學是物理學的另一個分支，也可以說是力學的一個子分支。這個物理學領域也處理運動，但在這裡我們不致力於尋找運動的原因。在運動學研究中，我們學習物體的各種運動型別，並從幾何角度找出物體運動的方向、速度和加速度的所有可能性。

因此，我們可以說，在運動學中，我們關注的是運動物體的運動方式，而不是關注原因，或者為什麼物體在運動？

在物體的運動學研究中，我們藉助速度、加速度和方向等因素而不是力和力矩來獲得結果。在這個力學領域，我們討論物體的位移以及物體在特定方向上位移變化的速率。此外，在運動學研究中，結果與物體的質量無關。

運動學的例子

• 有人向東走

• 一個包從建築物上掉下來

• 一輛腳踏車從0加速到100

• 軍艦發射的導彈

• 鐘錶的指標運動

• 一本書從桌子上掉下來

運動學的重要性

• 在我們的日常生活中，我們為了任何目的而旅行，但我們想要一個關於成本、距離等的近似概念。對於這種分析，我們可以使用運動學，其中我們可以考慮車輛的方向、距離和速度來計算所需時間和其他因素。

• 日復一日，人類對星際旅行的好奇心越來越強，對於這些活動，我們使用運動學方程來計算所需的方向和速度，以便安全旅行。

• 在田徑運動中，運動員利用運動學的規則和結果來實現鉛球或標槍的高分推進。

• 利用運動學定律，我們還可以設計具有合適動力和尺寸的機器人，並且藉助運動學方程進行一些計算，我們還可以遠端操作它們。

動力學與運動學之間的區別

動力學	運動學
研究運動的原因	研究運動的性質
研究運動的性質	研究具有位置、速度、方向和加速度的運動
物體的質量在動力學中很重要。	物體的質量沒有影響
不使用數學方程	3個運動學數學方程
考慮力	不受力的影響

結論

動力學和運動學都是力學的子分支，兩者都處理物體的運動。主要區別在於動力學側重於運動的原因，而運動學告訴我們運動的型別是什麼？

常見問題

Q1. 列出運動學的方程？

答：運動學具有以下運動方程，我們根據這些方程來檢查運動的型別。

• $\mathrm{u=v+at}$

• $\mathrm{s=ut+\frac{1}{2}at^2}$

• $\mathrm{v^2=u^2+2as}$

Q2. 力學有哪些型別？

答：力學有三種類型。

• 經典力學

• 量子力學

• 統計力學

Q3. 什麼是力學？

答：力學是物理學的一個分支。在這個科學分支中，我們處理物體靜止或運動的所有問題、可能性和原因。

Q4. 什麼是量子力學？

答：它是物理學的一個分支，研究的是分子和亞分子範圍內粒子的性質、行為和運動。

Q5. 什麼是動能？

答：動能是由於物體運動而產生的一種能量。物體的動能取決於該物體的質量和速度。

$\mathrm{K.E.=\frac{1}{2}mv^2}$

什麼是統計力學？

答：它是現代物理學的一個分支，用於研究具有許多自由度的物體的研究。在這個物理學分支中，我們學習機率論的重要性及其應用。此外，在這個部分中，我們還分析機械系統的平均行為。