資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究C++ 瓦里農平行四邊形的周長和麵積
瓦里農平行四邊形是由四邊形的每條邊的中點連線而成的。假設我們有一個四邊形 ABCD。每條邊的中點分別是 P、Q、R 和 S。如果我們連線所有中點，它將始終形成一個稱為瓦里農平行四邊形的平行四邊形 PQRS。
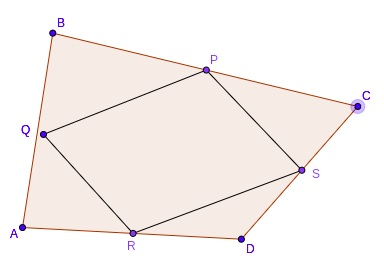
在本教程中，我們將討論如何根據給定的兩條對角線和四邊形的面積來找到瓦里農平行四邊形的周長和麵積，例如 -
Input: d1 = 6, d2 = 9, Area = 12 Output: Perimeter = 15 Area = 6 Input: d1 = 11, d2 = 13, Area = 32 Output: Perimeter = 24 Area = 16
求解方法
在三角形中，P 和 Q 分別是 AB、AC 的中點，
根據中點定理，PQ = (1/2)*AC
類似地，將定理應用於三角形 ADC，RS = (1/2)*BD，
所以 PQ=RS=(1/2)*AC 和 PS=QR=(1/2)*BD
PQRS 的周長 = AC + BD（對角線之和）
EF=GH=(1/2)*AC 和 EH=FG=(1/2)*BD
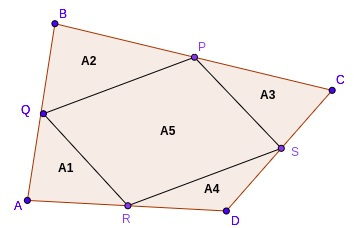
對於 PQRS 的面積，我們將圖形分成四個三角形，四個三角形的面積為，
A1=(1/4)*BAD 的面積
類似地，A2=(1/4)*ABC 的面積
A3=(1/4)*BCD 的面積
A4=(1/4)*ACD 的面積。
A1 + A2 + A3 + A4 = (1/4)*(ACD+ABC+BCD+BAD 的三角形面積)
= (¼) * 2* ABCD 的面積
= (½) * 四邊形 ABCD 的面積
現在 A1 + A2 + A3 + A4 = (½) * 四邊形 ABCD 的面積
這意味著 A5 = (½) * 四邊形 ABCD 的面積
所以平行四邊形 PQRS 的面積 = (½) * 四邊形 ABCD 的面積
現在我們可以透過使用 C++ 應用公式來找到 PQRS 的周長和麵積。
示例
以上方法的 C++ 程式碼
#include <bits/stdc++.h>
using namespace std;
int main(){
float d1 = 6, d2 = 9, area_ABCD = 12;
float area_PQRS = area_ABCD/2;
float perimeter = d1 + d2;
cout << "Area of parallelogram PQRS = " << area_PQRS << " and perimeter = " << perimeter;
return 0;
}
輸出
Area of parallelogram PQRS = 6 and perimeter = 15
結論
在本教程中，我們討論了瓦里農平行四邊形以及如何找到它的面積和周長。我們討論了使用中點定理推導平行四邊形的周長和麵積。我們還討論了此問題的 C++ 程式，我們可以使用 C、Java、Python 等程式語言來完成。希望本教程對您有所幫助。
142 次檢視
