資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法學交替子陣列計數
交替子陣列計數用於計算沒有兩個相鄰元素相同的子陣列的數量。我們也可以將這些子陣列稱為交替子陣列。
問題陳述
在瞭解什麼是“交替子陣列計數”之前，讓我們先看看什麼是子陣列和交替子陣列。
- 子陣列是陣列的一部分，透過移除陣列的一些或所有字首元素和一些或所有後綴元素形成。
-
將陣列分成多個子陣列時，可能存在兩個相鄰子陣列具有相同值的可能性。如果沒有任何兩個相鄰子陣列具有相同的值，則這些子陣列被稱為交替子陣列。
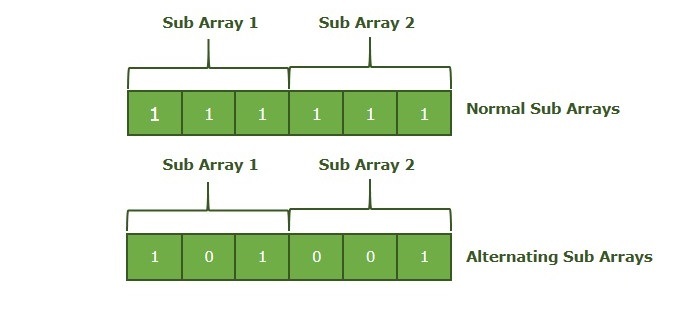
示例場景 1
Input: nums = [1, 1, 1 , 1]
Output:count = 4
交替子陣列 = [1]，[1]，[1]，[1]
示例場景 2
Input: nums = [1, 1, 1, 0]
Output:count = 5
交替子陣列 = [1]，[1]，[1]，[0]，[1, 0]
示例場景 3
Input: nums = [1, 0, 1, 0, 1]
Output: count = 9
交替子陣列 = [1]，[0]，[1]，[0]，[1]，[1, 0]，[0, 1]，[1, 0, 1]，[0, 1, 0]。
時間複雜度
計算交替子陣列的時間複雜度為 O(n)，其中 (n) 是陣列的長度。要使用各種程式語言解決此問題，請使用以下方法。
- 暴力法
- 動態規劃法
暴力法
這種方法是解決所有可能的解決方案問題的直接方法。
示例
該程式透過迭代整數向量並新增所有交替子陣列的長度來計算給定整數向量中交替子陣列的數量。
#include <iostream>
#include <vector>
using namespace std;
class Count {
public:
long long countAlternatingSubarrays ( vector<int>& nums ) {
long long ans = 1, s = 1;
for (int i = 1; i < nums.size(); ++i) {
s = nums[i] != nums[i - 1] ? s + 1 : 1;
ans += s;
}
return ans;
}
};
int main() {
Count X;
vector<int> nums = {1, 0, 1, 0, 1, 0};
cout << " Count of alternating subarrays = " << X.countAlternatingSubarrays(nums) << endl;
return 0;
}
輸出
Count of alternating subarrays = 21
import java.util.*;
public class Count {
public long countAlternatingSubarrays(int[] nums) {
long ans = 1, s = 1;
for (int i = 1; i < nums.length; ++i) {
s = (nums[i] != nums[i - 1]) ? s + 1 : 1;
ans += s;
}
return ans;
}
public static void main(String[] args) {
Count X = new Count();
int[] nums = {1, 0, 1, 0, 1, 0};
System.out.println("Count of alternating subarrays = " + X.countAlternatingSubarrays(nums));
}
}
輸出
Count of alternating subarrays = 21
def count_alternating_subarrays(nums):
ans = s = 1
for i in range(1, len(nums)):
s = s + 1 if nums[i] != nums[i - 1] else 1
ans += s
return ans
nums = [1, 0, 1, 0, 1, 0]
print("Count of alternating subarrays =", count_alternating_subarrays(nums))
輸出
Count of alternating subarrays = 21
動態規劃法
此方法用於透過將複雜問題分解成更簡單的子問題來解決複雜問題。
示例
以下是透過檢查每個可能的子陣列來計算給定整數向量中具有交替元素的子陣列數量的程式。
#include <iostream>
#include <vector>
using namespace std;
long long countAlternatingSubarrays(const vector<int>& nums) {
long long count = 0;
for (int i = 0; i < nums.size(); ++i) {
int sign = 0;
for (int j = i; j < nums.size(); ++j) {
if (j == i || nums[j] != nums[j - 1]) {
count++;
sign = !sign;
} else {
break;
}
}
}
return count;
}
int main() {
vector<int> nums = {1, 0, 1, 0, 1, 0};
cout << "Count of alternating subarrays = " << countAlternatingSubarrays(nums) << endl;
return 0;
}
輸出
Count of alternating subarrays = 21
import java.util.*;
public class Main {
public static long countAlternatingSubarrays(List <Integer> nums) {
long count = 0;
for (int i = 0; i < nums.size(); ++i) {
int sign = 0;
for (int j = i; j < nums.size(); ++j) {
if (j == i || !nums.get(j).equals(nums.get(j - 1))) {
count++;
sign = 1 - sign;
} else {
break;
}
}
}
return count;
}
public static void main(String[] args) {
List<Integer> nums = Arrays.asList(1, 0, 1, 0, 1, 0);
System.out.println("Count of alternating subarrays = " + countAlternatingSubarrays(nums));
}
}
輸出
Count of alternating subarrays = 21
def count_alternating_subarrays(nums):
count = 0
for i in range(len(nums)):
sign = 0
for j in range(i, len(nums)):
if j == i or nums[j] != nums[j - 1]:
count += 1
sign = not sign
else:
break
return count
nums = [1, 0, 1, 0, 1, 0]
print("Count of alternating subarrays = ", count_alternating_subarrays(nums))
輸出
Count of alternating subarrays = 21
更新於：2024年7月23日
瀏覽量：156
廣告