構造一個NFA，接受包含偶數個0或奇數個1的字串。

非確定有限自動機 (NFA) 也具有與 DFA 相同的五個狀態，但具有不同的轉移函式，如下所示：

δ: Q X Σ → 2^Q

其中，

• Q：稱為狀態的有限集。
• Σ：稱為字母表的有限集。
• δ：Q × Σ → Q 是轉移函式。
• q0 ϵ Q 是起始或初始狀態。
• F：最終或接受狀態。

問題

在字母表 Σ={0,1} 上構造 NFA。

解決方案

為這兩個條件設計兩個獨立的機器，如下所示：

• 僅接受奇數個1的NFA

• 僅接受偶數個0的NFA

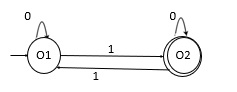
在字母表 Σ= {0,1} 上僅接受奇數個1的NFA。

它生成的語言是：

L={1,111,01,001,0111,0010,01110,…}

• 狀態 o1 在 0 上轉到 o1，在 1 上轉到狀態 o2。

• 狀態 o2 在 0 上轉到 o2，在 1 上轉到 o1。

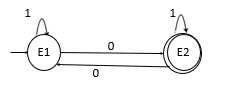
在字母表 Σ= {0,1} 上僅接受偶數個0的NFA

它生成的語言是：

L={100,1100,1010,1100010,……}

• 狀態 E1 在 1 上轉到 E1，在 0 上轉到 E2。

• 狀態 E2 僅在 1 上轉到 E2，在 0 上轉到 E1。

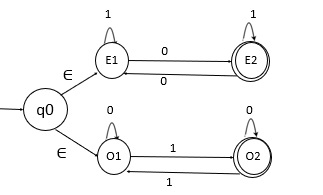
現在使用 epsilon 移動合併這兩個轉移圖。

**接受所有包含偶數個0或奇數個1的字串的NFA** 如下所示：

Bhanu Priya

更新於： 2021年6月15日

11K+ 瀏覽量

開啟您的職業生涯

透過完成課程獲得認證

開始學習