構造一個接受在字母表 {0,1} 上的偶長度迴文串的圖靈機 (TM)？

圖靈機 (TM) 是一個 7 元組 (Q, ∑, Γ, δ, q0, qaccept , qreject)。

其中，

  • Q 是一個有限的狀態集。

  • ∑ 是輸入字母表，不包含空白符號 t。

  • Γ 是帶字母表，其中 t ∈ Γ 且 ∑ ⊆ Γ。

  • δ: (Q × Γ) → (Q × Γ × {L, R}) 是轉移函式。

  • q0 ∈ Q 是起始狀態。

  • qaccept ∈ Q 是接受狀態。

  • qreject ∈ Q 是拒絕狀態，其中 qreject ≠ qaccept。

**為了接受在字母表 {0,1} 上的偶長度迴文串，**請按照以下步驟操作 -

  • 匹配第一個和最後一個元素並擦除它們，繼續執行相同的操作。一旦我們在沒有任何不匹配的情況下到達空串，則該字串是偶長度迴文串。

  • 對於偶長度迴文串，在機器執行並擦除第一個和最後一個元素且沒有遇到不匹配後，定義了一個 TM。之後，圖靈機接受該字串，該字串是偶長度迴文串。

假設字串為 -

110011

那麼，我們可以遇到三種情況，如下所示 -

**情況 1** - 如果起始和結束匹配，則擦除第一個和最後一個

擦除後 - 1001

**情況 2** - 如果起始和結束匹配，則擦除第一個和最後一個

擦除後 - 00

**情況 3** - 如果起始和結束匹配，則擦除第一個和最後一個零

擦除後剩餘 - 空串

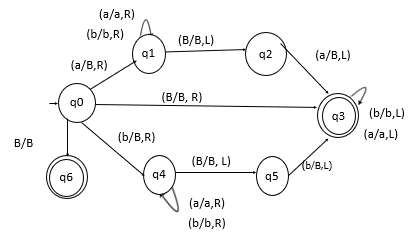
這是一個構造的圖靈機，它接受偶長度迴文串。

接受偶迴文串的 TM 的示意圖如下所示 -

更新於: 2021年6月16日

9K+ 瀏覽量

開啟你的 職業生涯

透過完成課程獲得認證

立即開始
廣告