圓的周長

---

簡介

圓的周長是邊界的長度。在幾何學中，圓是二維圖形之一。圓在現實生活中的應用非常廣泛，在建築和科學領域都發揮著重要作用。

現實生活中的例子有：結婚戒指、襯衫紐扣、方向盤、眼球晶狀體、摩天輪、車輛輪胎、光碟等。

它們有直徑和半徑。不同圓的半徑也不同。圓的直徑將圓分成兩個半圓。如果在平面上畫一個圓，則將平面分成兩個部分或區域，即內部和外部部分。這個二維圖形既有面積也有周長。

在本教程中，我們將學習圓周率 (π)、圓及其周長的定義，以及一些已解決的示例。

圓

圓是一種二維圖形，形狀為圓形，其邊界上的每個點到圓心的距離都相等。從圓心到圓邊界上任意一點的線段稱為圓的半徑。用 r 或 R 表示。

與半徑不同，如果線段的兩個端點都連線到圓的邊界，則稱為圓的弦。在圓中畫出的許多弦中，最大的弦稱為圓的直徑。用 d 或 D 表示。

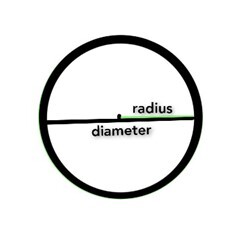
要找到圓的面積，我們需要將圓的半徑 r 乘以圓周率 (π) 的值。

注意

• 圓的直徑是圓的半徑的兩倍，

  $$\mathrm{直徑= 2 × 半徑}$$

• 圓的半徑是圓的直徑值的一半，

  $$\mathrm{半徑 = \frac{直徑}{2}}$$

圓的周長

如果測量圓的邊界，則該距離稱為圓的周長。周長也稱為圓的周界。簡單來說，周長就是圍繞圖形的路徑。它決定了圓的長度。如果半徑的兩倍或直徑相乘，則得到圓的周長。

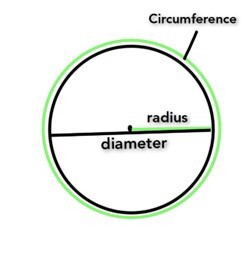
$$\mathrm{圓的周長\:=2πr\: 單位}$$

$$\mathrm{或 }$$

$$\mathrm{ πd\: 單位}$$

圓周率的定義

• 非終止十進位制或稱為無理數稱為圓周率。

• 用 π 表示。

• π 的數值為 $\mathrm{\frac{22}{7}}$ = 3.141592653589793238...

  因為圓的周長= πd

  $$\mathrm{π=\frac{圓的周長}{d}}$$,

• 它是圓的周長與圓的直徑之比。

解題示例

1)如果圓形按鈕的半徑為 0.21 釐米，則求按鈕的周長。

答案

已知

圓形按鈕的半徑 = 0.21 釐米。

$$\mathrm{圓的周長=2πr\: 單位}$$

$$\mathrm{按鈕的周長=2×\frac{22}{7}×0.21}$$

$$\mathrm{=44×0.03}$$

$$\mathrm{=1.32 釐米}$$

2)如果摩天輪的直徑為 56 米，則求摩天輪的周長。

答案

已知

摩天輪的直徑 = 56 米。

$$\mathrm{圓的周長=πd\: 單位}$$

$$\mathrm{摩天輪的周長=\frac{22}{7}×56}$$

$$\mathrm{ =22×8 }$$

$$\mathrm{=176 米。}$$

3)布拉德用泡沫塑膠為兒子製作了一個圓形輪子，周長為 220 釐米。求輪子的直徑。

答案

$$\mathrm{圓的周長=πd\: 單位}$$

$$\mathrm{摩天輪的周長=\frac{22}{7}×d}$$

$$\mathrm{220=\frac{22}{7}×d}$$

$$\mathrm{d=220 \times \frac{7}{22}}$$

$$\mathrm{輪子的直徑 = 70 米。}$$

4)佐伊買了一個呼啦圈，周長為 264 釐米。求呼啦圈的半徑。

答案

$$\mathrm{圓的周長=πd\: 單位}$$

$$\mathrm{呼啦圈的周長=\frac{22}{7}×d}$$

$$\mathrm{264 =\frac{22}{7}×d }$$

$$\mathrm{d =264×\frac{7}{22}}$$

$$\mathrm{呼啦圈的直徑 = 84\: 釐米。}$$

$$\mathrm{呼啦圈的半徑\: =\frac{ 直徑}{2}}$$

$$\mathrm{ =\frac{ 84}{2}}$$

呼啦圈的半徑 = 42 釐米。

5)如果圓形環的半徑為 35 釐米，則求環的周長。

答案

已知

環的半徑 = 35 釐米。

$$\mathrm{圓的周長=2πr\: 單位}$$

$$\mathrm{按鈕的周長=2×\frac{22}{7}×35 }$$

$$\mathrm{=44×5 }$$

$$\mathrm{=220\: 釐米。}$$

結論

• 圓是一種二維圖形，形狀為圓形，其邊界上的每個點到圓心的距離都相等。

• 從圓心到圓邊界上任意一點的線段稱為圓的半徑。

• 如果線段的兩個端點都連線到圓的邊界，則稱為圓的弦。

• 圓中最大的弦稱為圓的直徑。

• 如果測量圓的邊界，則該距離稱為圓的周長或圓的周界。

• 圓周率是圓的周長與圓的直徑之比，其數值為 3.141592653589793238....

常見問題

1. 什麼是球體？

圓是二維圖形。如果圓是一個三維圖形，是一個圓形固體，其表面上的每個點到其中心的距離都相等，則稱為球體。

2. 平面圖形和立體圖形有什麼區別？

• 平面圖形是二維幾何物體。這些型別的圖形包括正方形、矩形、圓形、三角形、六邊形、八邊形、五邊形等。

• 立體圖形是三維幾何物體。這些型別的立體圖形包括立方體、長方體、圓柱體、圓錐體、稜柱體、球體、半球體等。

3. 物體的面積和體積分別是什麼？

• 三維圖形佔據的空間區域稱為物體的體積。

• 二維圖形覆蓋的空間量稱為物體的面積。

4. 什麼是正多邊形？

在歐幾里得幾何中，多邊形是等角的並且具有全等邊。

例如：正方形、菱形、等邊三角形。

邊長不相等的多邊形是不規則多邊形。

例如：不等邊三角形、平行四邊形、等腰三角形、矩形等。

5. 圓的型別有哪些？

圓有三種類型，即全等圓、同心圓和相切圓。

6. 圓的標準方程是什麼？

圓的一般方程由下式給出：

$$\mathrm{(x-h)^2-(y-k)^2=r^2}$$

其中 (h,k) 是圓心的座標，r 是圓的半徑。

7. 圓是多邊形嗎？

平面的表面，用直線表示，稱為多邊形。

圓的邊界是曲線，沒有直線。因此，圓不能被認為是多邊形。