算術幾何數列

---

簡介

算術幾何級數是一個數列，其中每個元素的排列順序使得相鄰兩項的比值始終保持不變。

在數學中，數列是有序排列的一組數，數列中每個元素都對應著下一個元素的位置和值。數列是高等數學中計算無窮級數的基礎。在本教程中，我們將學習算術級數、第n項公式、算術級數n項之和以及一些已解決的例子。

數列

可以按一定順序排列的一組數，數列中的元素可以以任何方式重複。數列本身沒有值，而是每個元素都由一個公式定義，並可以根據該公式計算。級數可以分為三種類型：算術級數、幾何級數和調和級數。

算術數列 (AP)

也稱為“算術級數”，它是一個數列，其中每個元素的排列順序使得該數列中每一項與前一項的差值相同。級數中的每個元素都稱為“項”。

例如：2, 5, 8, 11, 14, 17, 20……

上述數列中每一項與其前一項或後一項的差值為3，這在算術級數中稱為“公差”。公差是算術數列中相鄰兩數的差值。我們也可以說，數列中的任何元素都可以透過從其相鄰元素中加或減一個特定數字來計算。

假設有一個數列：

x₁,x₂,x₃,x₄,x₅,...........x_n，其中x₁是第一項，x_n是最後一項。

設“a”為上述數列中的公差。

那麼：

$$\mathrm{x_2= x_1+a,}$$

$$\mathrm{x_3=x_2+a,}$$

$$\mathrm{x_4=x_3+a,}$$

$$\mathrm{\vdots}$$

$$\mathrm{x_n=x_{n-1}+a}$$

我們也可以將數列寫成：

算術級數的一般形式可以寫成

$$\mathrm{x_1,x_1+a,x_1+2a,x_1+3a,x_1+4a⋯,x_1+(n-1)a.}$$

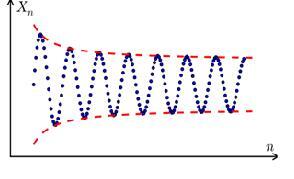
圖：有限數列的值用藍色繪製在圖上。

幾何數列 (GP)

一個數列，其中每個元素的排列順序使得該數列中每一項都可以透過將其前一項或後一項乘以或除以一個特定數字來計算。

例如：3, 9, 27, 81, 243, 729……

上述數列中每一項都是其前一項的倍數，這稱為數列的“公比”；在本例中為3。

讓我們考慮一個數列：

x₁,x₂,x₃,x₄,x₅,...........x_n，其中x₁是第一項，x_n是最後一項。

設“m”為上述數列中的公比。

那麼，我們也可以將數列寫成：

$$\mathrm{x_1,x_1 m,x_1 m^2,x_1 m^3,x_1 m^4\dotso,x_1 m^{n-1}.}$$

幾何級數的第n項公式

幾何級數的第n項由下式給出

$$\mathrm{x_n=x_1 r^{n-1}}$$

幾何級數的和，其首項為x_1，公比為r，由下式給出

$$\mathrm{S_n=\frac{x_1 (1-r^n)}{1-r}, where\: r≠1}$$

已解決的例子

1) 識別以下數列並找出數列的第n項。

• 4,15,26,41,.......

• 4, 12, 36, 108……

答案

a. 為了識別數列，我們首先應該找到相鄰項之間的關係。

$$\mathrm{15-4=11}$$

$$\mathrm{26-15=11}$$

$$\mathrm{41-26=11}$$

每個相鄰項之間的差值為11。因此，該數列是算術級數。

查詢算術級數第n項的公式為

$$\mathrm{第n項=x_1+(n-1)a}$$

$$\mathrm{x_1=4}$$

$$\mathrm{a=11}$$

那麼數列的第n項

$$\mathrm{=4+(n-1)11}$$

$$\mathrm{=11n-7}$$

因此，該數列的第n項為11n-7。

b. 為了識別數列，我們可以將除第一項外的每個元素除以前面的元素

$$\mathrm{12/4=3}$$

$$\mathrm{36/12=3}$$

$$\mathrm{108/36=3}$$

我們可以說，上述數列是公比為3的幾何級數。我們知道幾何級數的第n項可以由下式給出

$$\mathrm{\mathrm{x_n=x_1 r^{n-1}}}$$

將值代入方程，我們得到

$$\mathrm{x_n=4×3^{n-1}}$$

$$\mathrm{x_n=4×3^n×3^{-1}}$$

$$\mathrm{x_n=4×3^n×\frac{1}{3}}$$

$$\mathrm{x_n=\frac{4}{3}×3^n}$$

因此，給定數列的第n項 $\mathrm{x_n=\frac{4}{3}×3^n}$

2) 找出以下級數的項數。

• 1, 5, 9, 13, 17, ……….125

• 1, 2, 4, 8, 16, …………1024

答案

a. 要找出上述數列的項數，我們首先需要確定級數的型別

$$\mathrm{5-1=4}$$

$$\mathrm{9-5=4}$$

$$\mathrm{13-9=4}$$

每個相鄰項之間的差值為4。因此，該數列是算術級數。

查詢算術級數第n項的公式為

$$\mathrm{第n項= x_1+(n-1)a}$$

$$\mathrm{ x_1=1}$$

$$\mathrm{a=4}$$

那麼數列的第n項

$$\mathrm{125=1+(n-1)4}$$

$$\mathrm{125 =4n-3}$$

$$\mathrm{4n=128}$$

$$\mathrm{n=32}$$

給定數列中有32項。

b. 為了識別數列，我們可以將除第一項外的每個元素除以前面的元素

$$\mathrm{2/1=2}$$

$$\mathrm{4/2=2}$$

$$\mathrm{8/4=2}$$

我們可以說，上述數列是公比為3的幾何級數。我們知道幾何級數的第n項可以由下式給出

$$\mathrm{x_n=x_1 r^{n-1}}$$

將值代入方程，我們得到

$$\mathrm{1024=1×2^{n-1}}$$

$$\mathrm{1024=1×2^{n-1}}$$

我們可以將1024寫成2¹⁰

$$\mathrm{2^{10}=2^{n-1}}$$

因為底數相同，所以我們可以將指數相等

$$\mathrm{10=n-1}$$

$$\mathrm{n=11}$$

因此，給定數列中有11項。

結論

數列是可以按一定順序排列的一組數，數列中的元素可以以任何方式重複。算術數列是一個數列，其中每個元素的排列順序使得該數列中每一項與前一項的差值相同。幾何級數是一個數列，其中每個元素的排列順序使得相鄰兩項的比值始終保持不變。

算術級數和幾何級數的區別。

算術級數	幾何級數
算術級數是一個數列，其中每個元素與前一項的差值相同。	幾何級數是一個數列，其中數列中的每一項都是其前一項的倍數。
算術級數由相鄰項之間的公差定義。	幾何級數由相鄰項之間的公比定義。
算術級數是一個線性數列	幾何級數是一個指數數列。
算術級數示例：	幾何級數示例： 10, 20, 40, 80,....
10, 30, 50, 70……

常見問題解答 (FAQ)

1. 列舉代數中級數的型別。

代數中級數的型別包括：

• 算術級數 (AP)

• 幾何級數 (GP)

• 調和級數 (HP)

2. 什麼是調和級數？

它是構成算術級數的數字的倒數的數列。

3. 如何計算公比小於1的無窮級數？

具有無窮多項和公比小於1的幾何級數可以透過以下公式計算：

$\mathrm{S=\frac{a}{1-r}}$，其中“a”是首項，“r”是公比。

4. 數列和級數有什麼區別？

數列是基於定義屬性的有序數字。例如2, 4, 6, 8……級數是有序排列的數字之和。例如2+4+6+8……

5. AP和HP之間有什麼關係？

AP各項的倒數構成一個HP。