資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚學
法律學拓撲排序
有向無環圖的拓撲排序是頂點的線性排序。對於有向圖的每條邊 U-V，頂點 u 將在排序中排在頂點 v 之前。
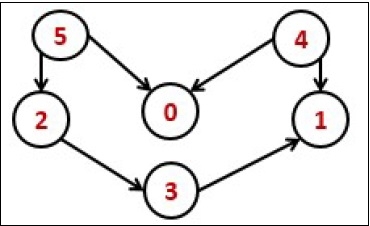
如我們所知，源頂點排在目標頂點的後面，因此我們需要使用一個棧來儲存先前的元素。完成所有節點後，我們可以簡單地從堆疊中顯示它們。
輸入輸出
Input: 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 1 1 0 0 0 0 1 0 1 0 0 0 Output: Nodes after topological sorted order: 5 4 2 3 1 0
演算法
topoSort(u, visited, stack)
輸入 − 開始頂點 u、用於跟蹤已訪問或未訪問的節點的陣列。用於儲存節點的堆疊。
輸出 − 在棧中按拓撲順序對頂點進行排序。
Begin mark u as visited for all vertices v which is adjacent with u, do if v is not visited, then topoSort(c, visited, stack) done push u into a stack End
performTopologicalSorting(Graph)
輸入 − 給定的有向無環圖。
輸出 − 節點序列。
Begin initially mark all nodes as unvisited for all nodes v of the graph, do if v is not visited, then topoSort(i, visited, stack) done pop and print all elements from the stack End.
示例
#include<iostream>
#include<stack>
#define NODE 6
using namespace std;
int graph[NODE][NODE] = {
{0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0},
{0, 0, 0, 1, 0, 0},
{0, 1, 0, 0, 0, 0},
{1, 1, 0, 0, 0, 0},
{1, 0, 1, 0, 0, 0}
};
void topoSort(int u, bool visited[], stack<int>&stk) {
visited[u] = true; //set as the node v is visited
for(int v = 0; v<NODE; v++) {
if(graph[u][v]) { //for allvertices v adjacent to u
if(!visited[v])
topoSort(v, visited, stk);
}
}
stk.push(u); //push starting vertex into the stack
}
void performTopologicalSort() {
stack<int> stk;
bool vis[NODE];
for(int i = 0; i<NODE; i++)
vis[i] = false; //initially all nodes are unvisited
for(int i = 0; i<NODE; i++)
if(!vis[i]) //when node is not visited
topoSort(i, vis, stk);
while(!stk.empty()) {
cout << stk.top() << " ";
stk.pop();
}
}
main() {
cout << "Nodes after topological sorted order: ";
performTopologicalSort();
}輸出
Nodes after topological sorted order: 5 4 2 3 1 0
更新於：2020 年 6 月 16 日
6 千次 + 瀏覽
廣告