資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學什麼是二義性文法？
產生相同句子的左推導（或右推導）不止一種的文法稱為二義性文法。
示例 − 驗證以下文法是否二義性。
E → E+E|E $\ast$ E|id
解答
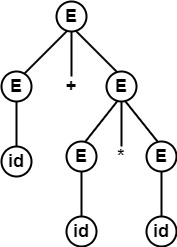
對於字串 id + id * id，存在兩棵不同的語法樹。
E ⇒lm $\underline{E}$+E
⇒ id+ $\underline{E}$
⇒ id+$\underline{E}$ $\ast$ E
⇒ id+id $\ast$ $\underline{E}$
⇒ id+id $\ast$ id
E ⇒lm $\underline{E}$ $\ast$ E
⇒ $\underline{E}$+E $\ast$ E
⇒ id+ $\underline{E}$ $\ast$ E
⇒ id+id $\ast$ $\underline{E}$
⇒ id+id $\ast$ id
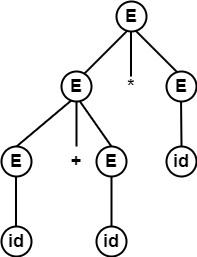
因此，同一個字串使用了兩種不同的左推導生成。每種推導都有不同的語法樹。
∴ 字串 id + id * id 存在兩棵不同的語法樹。
∴ 文法是二義性的。
將二義性文法轉換為非二義性文法
在其右部包含一個給定非終結符多次出現的產生式是二義性產生式。
示例 − E → $\underline{E}$ * $\underline{E}$
它在右部包含兩個 E。
可以透過引入一個新的非終結符將這些非終結符中最右邊的非終結符移動到語法樹的更下方，從而將這些型別的二義性產生式轉換為非二義性產生式。
示例1 − 考慮以下文法
E → E+E|E $\ast$ E|(E)| id
將這個二義性文法轉換為非二義性文法。
解答
步驟1 − 引入一個非終結符 T（項），它不能再進一步分解為兩個項的加法。
E → E+T | T T → E * E | (E) |id
步驟2 − 由於我們有產生式 E → T。用 T 代替 E 得到
T→T∗T
引入另一個非終結符 F（因子），它不能進一步分解，也不能是兩個數字的乘積。
用 F 代替 T 得到，
T → T * F | F F → (E) | id
∴ 非二義性文法將是
E → E+T | T T → T * F | F F → (E) | id
示例2 − 證明以下文法對於字串 if c then if c2 then s1 else s2 是二義性的。
<statement> →if<cond> then<statement> | if<cond> then<statement> else<statement>
|另一個語句
將其轉換為非二義性文法。
解答
給定的文法是二義性的，因為對於同一個字串存在兩棵不同的語法樹，因為 else 條件可以屬於任何 if 語句。
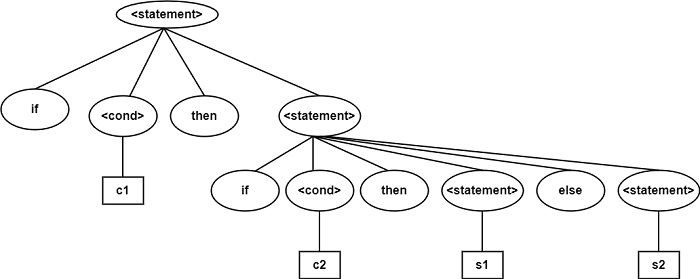
在上圖的語法樹中，else 屬於第二個 if。
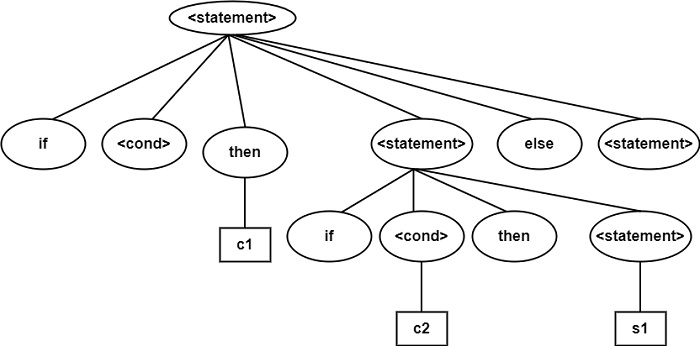
在上圖的語法樹中，else 屬於第一個 if。
轉換為非二義性文法
非二義性文法將是 −
<statement>→<match−statement>|<Unmatch−statement> <match−statement>→if<cond>then<match−statement>else <match−statement>| other−statement <Unmatch−statement>→if<cond>then<statement>| if<cond>then <match−statement>else<Unmatch Statement>
17K+ 次瀏覽
