地球逃逸速度

---

簡介

我們常常好奇，任何物體如何才能擺脫地球的引力。地球的質量為$\mathrm{5.972\:\times\:10^{24}\:kg}$，相當巨大，其引力也應該非常強大。

這就引出了一個可能性問題，答案是火箭利用了我們熟知的巨大速度——逃逸速度。憑藉這種作用力，火箭能夠克服地球強大的引力，飛向太空。

什麼是逃逸速度及其單位？

逃逸速度是指物體從地球表面脫離所需的最小速度。逃逸速度也稱為逃逸速度，它使物體能夠擺脫引力（Haug, 2021）。

逃逸速度的單位是米每秒，記作$\mathrm{m/s}$，與逃逸速度的SI單位相同。逃逸速度的量綱公式表示為[$\mathrm{M^0L^1T^{-1}}$]。

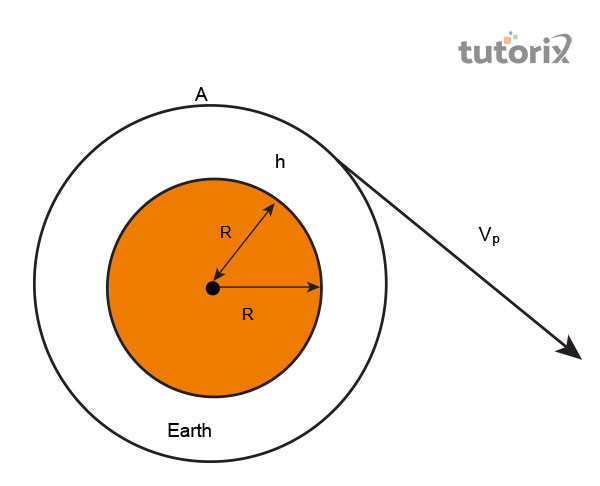
圖1：逃逸速度

什麼速度被稱為逃逸速度？

為了理解與逃逸速度相關的速度，我們需要將地球視為一個巨大的質量體。更重要的是，要理解想要擺脫引力的物體需要考慮地球的質量及其與想要逃逸的物體之間的距離 (Müller, 2018)。

因此，速度將基於這兩個方面推匯出來。這反過來表明，隨著想要逃逸的物體的質量增加和距離減小，逃逸速度必然要更大。

逃逸速度的推導

為了推導逃逸速度，需要考慮物體及其速度。當物體開始運動時，其動能和重力勢能被認為是零。這反過來定義了，根據能量守恆原理，可以表示為

(K+Ug)i = (K+Ug)f

其中，K是動能，其公式為$\mathrm{1/2\:m\:v^2}$。字母U表示重力勢能，表示為$\mathrm{(GMm)/r\:(Qrg.northwestern,\:2022)}$。因此，所需的最小逃逸速度用$\mathrm{V_{e}}$表示，等於$\mathrm{\sqrt{2gr}}$，又等於($\mathrm{\sqrt{2GM/r}}$)。在這個等式中，g表示萬有引力常數，其中g分別用$\mathrm{GM/r^2}$表示。

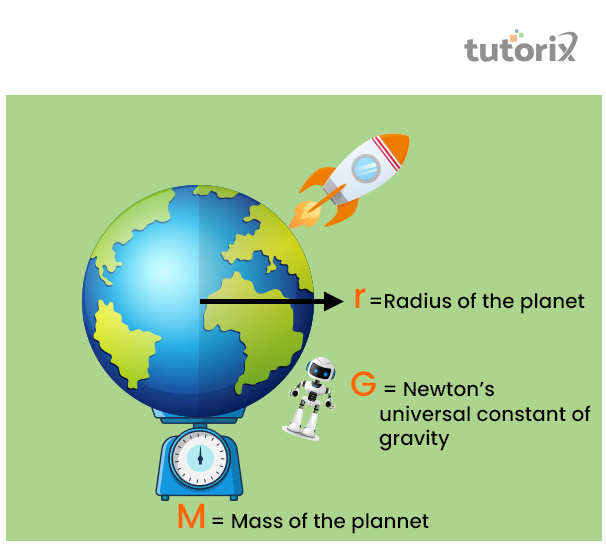
圖2：逃逸速度的推導

地球逃逸速度的值

逃逸速度的值可以透過包括地球的重力加速度（$\mathrm{g\:=\:9.8m/s^2}$）、地球半徑（$\mathrm{R\:=\:6.4\:\times\:10^6m}$）（Letstalkscience, 2022）等相應的值來確定。因此，逃逸速度的值由$\mathrm{v_e\:=\:11.2\:km/s}$確定，這可以看作是一個近似值。

圖3：逃逸速度的值

不同天體的逃逸速度

需要注意的是，由於逃逸速度主要取決於行星的質量以及行星與試圖逃逸的物體之間存在的距離，因此太陽系內不同行星的逃逸速度會發生變化 (Vanderbilt, 2022)。

例如，木星的逃逸速度最高，而火星的逃逸速度最低。然而，太陽的逃逸速度為$\mathrm{618 km/s}$，月球的逃逸速度為$\mathrm{2.38 km/s}$ (Scienceabc, 2022)。此外，穀神星的逃逸速度分別為$\mathrm{0.64km/s}$。

結論

在本教程中，我們注意到，我們對逃逸速度的概念進行了深入的研究。我們常常感到困惑的是，為什麼質量遠小於地球的火箭能夠輕易逃離地球表面。然而，我們需要理解的是，其中蘊含著簡單的物理原理，即逃逸速度取決於質量和距離。因此，可以理解的是，不同天體的逃逸速度是不同的。

常見問題

Q1. 軌道速度和逃逸速度之間有什麼區別？

軌道速度和逃逸速度之間存在顯著差異。軌道速度是指到達任何行星或太陽系內任何恆星軌道所需的速率。另一方面，逃逸速度是指離開相應軌道所需的速率。

Q2. 逃逸速度和軌道速度這兩個概念之間有什麼關係？

對於任何物體，逃逸速度是指與軌道內速度相關的函式。軌道速度的乘積及其2的平方根可以達到逃逸速度。此外，還可以獲得控制物體的引力。例如，在我們的太陽系中，木星似乎具有最高的逃逸速度，而水星似乎具有最低的逃逸速度。

Q3. 逃逸速度取決於哪些因素？

逃逸速度取決於地球上特定物體的因素包括地球的質量以及用符號ρ表示的平均密度。但是，需要注意的是，逃逸速度不取決於發射物體的方向及其質量。