資料結構
網路
關係資料庫管理系統(RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學Tarjan演算法求解強連通分量
Tarjan演算法用於查詢有向圖的強連通分量。該演算法只需要一次深度優先搜尋(DFS)遍歷即可實現。
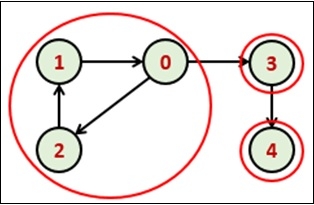
使用DFS遍歷，我們可以找到森林的DFS樹。從DFS樹中，可以找到強連通分量。當找到這樣的子樹的根時，我們可以顯示整個子樹。該子樹就是一個強連通分量。
輸入和輸出
Input: Adjacency matrix of the graph. 0 0 1 1 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 Output: The strongly connected components: 4 3 1 2 0
演算法
findComponent(u, disc, low, stack, stackItemFlag)
輸入：起始節點、發現時間、low值。disc將儲存頂點的發現時間，low將儲存關於子樹的資訊。stack用於儲存頂點，另一個標誌陣列用於跟蹤哪個節點在stack中。
輸出：顯示強連通分量(SCC)。
Begin time := 0 //the value of time will not be initialized for next function calls set disc[u] := time+1 and low[u] := time + 1 time := time + 1 push u into stack stackItemFalg[u] := true for all vertex v which is adjacent with u, do if v is not discovered, then fincComponent(v, disc, low, stack, stackItemFalg) low[u] = minimum of low[u] and low[v] else if stackItemFalg[v] is true, then low[u] := minimum of low[u] and disc[v] done poppedItem := 0 if low[u] = disc[u], then while u is not in the stack top, do poppedItem := top of stack display poppedItem stackItemFlag[poppedItem] := false pop item from stack done poppedItem := top of stack display poppedItem stackItemFlag[poppedItem] := false pop item from stack End
strongConComponent(graph)
輸入：給定的圖。
輸出：所有強連通分量。
Begin initially set all items in the disc array to undiscovered for all elements in low to φ and mark no item is stored into the stack for all node i in the graph, do if disc[i] is undiscovered, then findComponent(i, disc, low, stack, stackItemFlag) End
示例
#include<iostream>
#include<stack>
#define NODE 5
using namespace std;
int graph[NODE][NODE] = {
{0, 0, 1, 1, 0},
{1, 0, 0, 0, 0},
{0, 1, 0, 0, 0},
{0, 0, 0, 0, 1},
{0, 0, 0, 0, 0}
};
int min(int a, int b) {
return (a<b)?a:b;
}
void findComponent(int u, int disc[], int low[], stack<int>&stk, bool stkItem[]) {
static int time = 0;
disc[u] = low[u] = ++time; //inilially discovery time and low value is 1
stk.push(u);
stkItem[u] = true; //flag as u in the stack
for(int v = 0; v<NODE; v++) {
if(graph[u][v]) {
if(disc[v] == -1) { //when v is not visited
findComponent(v, disc, low, stk, stkItem);
low[u] = min(low[u], low[v]);
} else if(stkItem[v]) //when v is in the stack, update low for u
low[u] = min(low[u], disc[v]);
}
}
int poppedItem = 0;
if(low[u] == disc[u]) {
while(stk.top() != u) {
poppedItem = stk.top();
cout << poppedItem << " ";
stkItem[poppedItem] = false; //mark as item is popped
stk.pop();
}
poppedItem = stk.top();
cout << poppedItem <<endl;
stkItem[poppedItem] = false;
stk.pop();
}
}
void strongConComponent() {
int disc[NODE], low[NODE];
bool stkItem[NODE];
stack<int> stk;
for(int i = 0; i<NODE; i++) { //initialize all elements
disc[i] = low[i] = -1;
stkItem[i] = false;
}
for(int i = 0; i<NODE; i++) //initialize all elements
if(disc[i] == -1)
findComponent(i, disc, low, stk, stkItem);
}
int main() {
strongConComponent();
}輸出
4 3 1 2 0
更新於：2020年6月16日
2K+ 次瀏覽
廣告