資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學Swift 實現線性查詢演算法的程式
在 Swift 中，線性查詢演算法是最簡單的查詢演算法。線上性查詢演算法中，搜尋從索引 0 開始，逐個檢查給定陣列/序列中的所有元素，直到找到所需的元素。如果找到所需的元素，則返回該元素的索引。如果找不到所需的元素，則返回 null。
例如 −
我們有一個元素 M = 13，現在我們使用線性查詢演算法在以下陣列中搜索 M −
線性查詢演算法從索引 0 開始，將 M=13 與每個元素逐個比較，如下面的影像所示 −
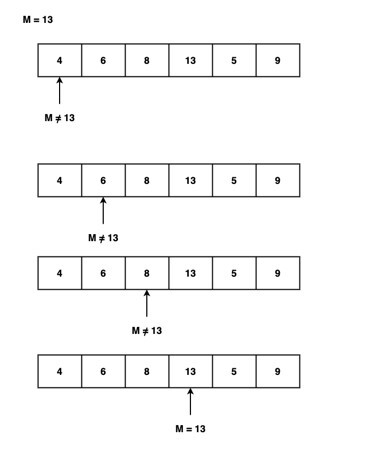
在上面的影像中，在給定陣列中找到了 M 元素，因此它返回索引 3。否則，它將返回“元素未找到”。
演算法
步驟 1 − 建立一個函式，該函式接受兩個引數：一個泛型型別為“M”的元素陣列和一個型別為“M”的目標元素。
步驟 2 − 在函式內部，執行一個 for 迴圈，該迴圈遍歷陣列的每個元素，並檢查它們是否等於目標元素。
步驟 3 − 如果目標元素等於當前元素，則返回該元素的索引。
步驟 4 − 如果在給定陣列中找不到目標元素，則此函式返回 nil。
步驟 5 − 在函式外部建立一個數組和一個目標元素。
步驟 6 − 現在呼叫該函式並將陣列和目標元素傳遞給它以獲取結果。
步驟 7 − 列印輸出。
示例 1
在下面的示例中，我們建立一個名為 linearSearchAlgorithm 的函式來實現線性查詢演算法。此函式接受兩個引數：陣列 = [2, 4, 19, 5, 23, 7, 16, 5, 18] 和目標元素 = 23。現在，該函式從索引 0 開始執行一個 for 迴圈，並使用 == 運算子檢查當前元素是否等於目標元素 = 23。如果當前元素等於目標元素，則返回當前元素的索引。否則，移動到下一個元素。此過程持續到陣列的末尾。如果找不到目標，則此函式返回 nil。在本例中，在給定陣列中找到了目標元素。因此，我們得到“元素 23 位於索引 4”作為輸出。
import Foundation
import Glibc
func linearSearchAlgorithm<M: Equatable>(_ array: [M], _ element: M) -> Int? {
for x in 0..<array.count {
if array[x] == element {
return x
}
}
return nil
}
let arr = [2, 4, 19, 5, 23, 7, 16, 5, 18]
let ele = 23
if let indexValue = linearSearchAlgorithm(arr, ele) {
print("Element \(ele) is found at index \(indexValue)")
} else {
print("Element \(ele) is not found in the given array.")
}
輸出
Element 23 is found at index 4
示例 2
在下面的示例中，我們將建立一個名為 linearSearchAlgorithm 的函式來實現線性查詢演算法。此函式接受兩個引數：陣列 = [2, 4, 6, 12, 56, 3, 8] 和目標元素 = 6。現在，該函式使用 enumerated() 方法迭代陣列的每個元素。enumerated() 方法在每次迭代中返回一個包含元素索引和值的元組。因此，如果目標元素與當前元素匹配，則此函式返回該元素的索引。否則，返回 nil。在本例中，在給定陣列中找到了目標元素。因此，函式返回 indexValue = 2。
import Foundation
import Glibc
func linearSearchAlgorithm<M: Equatable>(_ array: [M], _ element: M) -> Int? {
for (indexValue, Celement) in array.enumerated() {
if Celement == element {
return indexValue
}
}
return nil
}
let arr = [2, 4, 6, 12, 56, 3, 8]
let ele = 6
if let indexValue = linearSearchAlgorithm(arr, ele) {
print("Element \(ele) is found at index \(indexValue)")
} else {
print("Element \(ele) is not found in the given array.")
}
輸出
Element 6 is found at index 2
結論
這就是我們如何實現線性查詢演算法。線性查詢演算法可以處理已排序或未排序的序列。線性查詢演算法的最佳執行時間為 1，而最差執行時間為 n，其中 n 表示搜尋陣列中的元素總數。雖然線性查詢演算法是最簡單的演算法，但它不適用於較大的陣列。
486 次瀏覽
