質點直線運動

---

引言

如果粒子的位置隨時間和周圍環境而變化，則該粒子的本體就被認為是運動的。從數學角度來看，運動可以用特定參考系中的位移、速度和加速度來描述。位移、速度和加速度嚴格限制在一個方向上。

什麼是質點直線運動？

運動是我們日常生活中的一種重要現象，主要體現在各種電子裝置中。質點直線運動主要在座標軸上適用。簡單來說，質點直線運動主要用於對粒子運動進行適當的描述 (Nyobe 等人，2021)。

從數學角度來看，線性運動以及質點直線運動是描述粒子運動最常用的方法。

質點直線運動的應用

質點直線運動的應用常見於公共場所的電梯中。此外，測量由於自由落體運動而產生的物體的重力也是質點直線運動的一個完美例子。

質點直線運動應用的其他重要方面常見於兒童滑梯以及通常以飛行方式觀察到的行星運動，這也是質點直線運動的完美例子。為了維持和測量物體的速度，可以透過“具有非均勻加速度的直線運動”來測量。

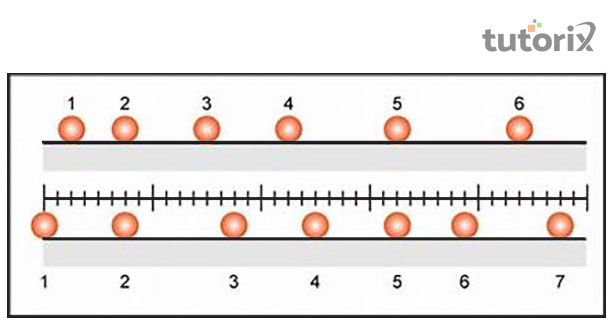
圖1：直線運動的應用

測量物體非均勻加速度的運動是速度變化的獨特例子。速度是一種線性型別，完全隨時間變化，這就是為什麼直線穿過直線的原因。兩種不同粒子的運動都屬於特定中心力的作用，例如靜電力，這很容易透過使用質點直線運動來測量力。

質點直線運動的型別

直線運動分為三種不同的型別：勻速運動，主要作用於零加速度；“勻加速運動”，主要指恆定的非零加速度；此外，屬於非勻加速運動的運動是最重要的直線運動型別之一。這種運動是重力下的自由落體運動以及與彈簧粒子大規模連線的簡諧運動。所有型別的直線運動都分別用於屬於任何其他電氣裝置的不同電場或磁場的粒子中。“勻速直線運動”是指物體以恆定速度和零加速度運動的情況 (Kailasham & Khair, 2022)。“勻加速直線運動”可以出現在粒子以大於零的恆定加速度運動的情況下。最後，如果粒子以不一致的速度以及快速變化的加速度運動，“具有非均勻加速度的直線運動”就會發生。

質點直線運動的功能

距離和位移是一個重要的概念，主要適用於質點直線運動。這裡，距離是指在旅途中由電運動覆蓋的總長度。運動的位移可以定義為路徑起始位置和最終位置之間的距離。

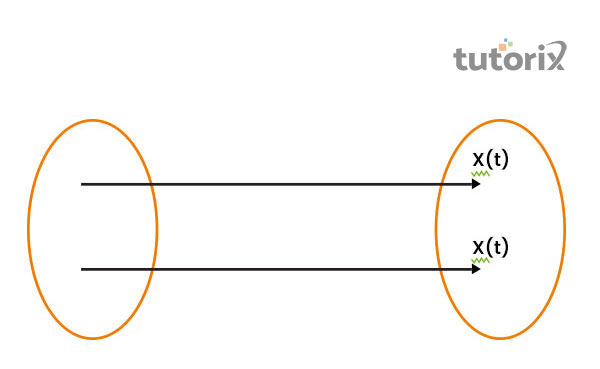
圖2：質點直線運動

質點直線運動也常被稱為直線運動，因為粒子是直線運動的。在上圖中，x/(t) 表示沿運動方向移動的粒子的位置，公式中的 T 表示運動的初始時間 (Durey & Bush, 2021)。

在粒子的最終位置，時間是從運動的初始時間和最終時間計算出來的。質點直線運動主要用於測量粒子的位移、速度和加速度。

質點直線運動最常見的應用分別體現在許多不同數學問題的各種問題中。透過應用質點直線運動，粒子的位置和位移、速度以及運動學問題的評估主要接受匯出的方程 (Schnitzer, 2022)。為了測量不同粒子的速度，質點直線運動經常被使用。

粒子的速度可以透過測量總行程距離乘以所用總時間來計算。透過應用質點直線運動，也可以透過從粒子的最終位置減去粒子的初始位置來測量粒子的速度，整個計算結果除以旅途中所用的總時間 (Diehl, 2020)。

• 電梯的運動是質點直線運動的一個完美例子。

結論

不同型別的運動都可以歸類為質點直線運動。旋轉運動是一種重要的運動型別，主要涉及特定物體的運動，該物體提供圍繞旋轉軸發生的圓周運動。這種特殊的運動通常透過地球的旋轉來觀察。振盪運動是另一個重要的類別，它反映了週期性運動。當孩子玩鞦韆時，通常會看到這種特殊的運動。

參考文獻

期刊

Diehl, E. (2020). The Engineering Dynamics Course Companion, Part 1: Particles: Kinematics and Kinetics. Synthesis Lectures on Mechanical Engineering, 5(4), 1-245.

Durey, M., & Bush, J. W. (2021). Classical pilot-wave dynamics: The free particle. Chaos: An Interdisciplinary Journal of Nonlinear Science, 31(3), 033136. Retrieved from: https://aip.scitation.org

Kailasham, R., & Khair, A. S. (2022). Chaotic dynamics of an autophoretic particle. arXiv preprint arXiv:2203.01988. Retrieved from: https://arxiv.org

Nyobe, S., Campillo, F., Moto, S., & Rossi, V. (2021). The one step fixed-lag particle smoother as a strategy to improve the prediction step of particle filtering. Retrieved from: https://hal.inria.fr

Schnitzer, O. (2022). Weakly nonlinear dynamics of a chemically active particle near the threshold for spontaneous motion. Part 1: Adjoint method. arXiv preprint arXiv:2205.06136. Retrieved from: https://arxiv.org

網站

conceptualdynamics (2022), Different types of motion, Available at: http://www.conceptualdynamics.com [Accessed on 10th June 2022]