資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究Python 程式構建給定表示式的表示式樹
表示式樹是指葉子節點包含要操作的值，而內部節點包含對葉子節點執行的運算子的樹。
例如：4 + ((7 + 9) * 2) 將具有如下所示的表示式樹 -
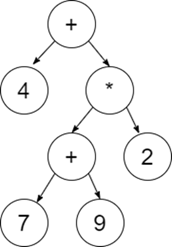
解決此問題的方法
為了為給定表示式構建表示式樹，我們通常使用棧資料結構。最初，我們遍歷給定的字尾表示式並遵循以下步驟 -
- 如果我們在給定表示式中得到一個運算元，則將其壓入棧中。它將成為表示式樹的根。
- 如果一個運算子在表示式中得到兩個值，則將其作為子節點新增到表示式樹中，並將它們壓入當前節點。
- 重複步驟 1 和步驟 2，直到我們完成給定表示式。
示例
class stack: def __init__(self): self.arr = [] def push(self, data): self.arr.append(data) def pop(self): try: return self.arr.pop(-1) except: pass def top(self): try: return self.arr[-1] except: pass def size(self): return len(self.arr) # node class for expression tree class node: def __init__(self, data): self.data = data self.left = None self.right = None # expression tree class class exp_tree: def __init__(self, postfix_exp): self.exp = postfix_exp self.root = None self.createTree(self.exp) def isOperator(self, char): optr = [" ", "-", "*", "/", "^"] if char in optr: # if given char is operator return True # then return true return False # else return false def createTree(self, exp): s = stack() # store those operator node whose any child node is NULL self.root = node(exp[-1]) # last character of postfix expression is always an operator s.push(self.root) # travel on rest of the postfix expression for i in "".join(reversed(exp[:-1])): curr_node = s.top() if not curr_node.right: # if right node of current node is NULL temp = node(i) curr_node.right = temp if self.isOperator(i): s.push(temp) else: # if left node of current node is NULL temp = node(i) curr_node.left = temp # if no child node of current node is NULL s.pop() # pop current from stack if self.isOperator(i): s.push(temp) def inorder(self, head): # inorder traversal of expression tree # inorder traversal = > left, root, right if head.left: self.inorder(head.left) print(head.data, end=" ") if head.right: self.inorder(head.right) def infixExp(self): # inorder traversal of expression tree give infix expression self.inorder(self.root) print() if __name__ == "__main__": postfixExp = "ab ef*g*-" et = exp_tree(postfixExp) et.infixExp()
執行以上程式碼將生成如下輸出：
輸出
(a + b - e * f * g)
解釋
從給定表示式構建樹將生成這樣的輸出：運算元將成為節點的根，其餘數字將成為表示式樹的子節點。
更新於： 2021 年 2 月 23 日
2K+ 瀏覽量
廣告