使用Python查詢最大機率路徑的程式

假設我們有一個具有n個節點的無向加權圖（節點編號從0開始）。此圖使用邊列表作為輸入給出，對於每條邊e，它都有一個遍歷該邊的成功機率probability[e]。我們還有起始節點和結束節點，我們必須找到從起始節點到結束節點的成功機率最大的路徑，並返回其成功機率。如果找不到任何路徑，則返回0。

因此，如果輸入類似於：

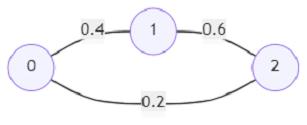
則輸出將為0.24，因為從節點0到2有兩條路徑，一條機率為0.2，另一條透過節點1，機率為0.4*0.6 = 0.24，這是最大值。

為了解決這個問題，我們將遵循以下步驟：

  • g := 從給定的邊列表建立圖，並使用機率值作為權重

  • q := 一個佇列資料結構

  • 將(start, 1)插入q

  • visited := 一個對映，用於儲存已訪問的節點

  • 當q不為空時，執行以下操作：

    • (node, prob) := q的第一個專案，並將其從q中刪除

    • 如果visited[node] > prob，則

      • 進入下一次迭代

    • 否則，

      • visited[node] := prob

    • 對於g[node]中的每個相鄰節點adj和機率nextProb，執行以下操作：

      • 如果visited[adj] < prob * nextProb，則

        • 將(adj, prob * nextProb)插入q的末尾

  • 返回visited[end]

讓我們看看下面的實現，以便更好地理解：

示例

 線上演示

from collections import defaultdict, deque
def solve(edges, probability, start, end):
   g = defaultdict(list)
   for i in range(len(edges)):
      src, dst = edges[i][0], edges[i][1]
      prob = probability[i]
      g[src].append((dst, prob))
      g[dst].append((src, prob))
   q = deque()
   q.append((start, 1))
   visited = defaultdict(int)
   while q:
      node, prob = q.popleft()
      if visited[node] > prob:
         continue
      else:
         visited[node] = prob
      for adj, nextProb in g[node]:
         if visited[adj] < prob * nextProb:
            q.append((adj, prob * nextProb))
   return visited[end]
edges = [[0,1],[1,2],[0,2]]
probability = [0.5,0.5,0.2]
start = 0
end = 2
print(solve(edges, probability, start, end))

輸入

[[0,1],[1,2],[0,2]], [0.5,0.5,0.2], 0, 2

輸出

0.25

更新於：2021年5月29日

428 次瀏覽

開啟您的職業生涯

完成課程獲得認證

開始
廣告
© . All rights reserved.