使用 Python 將兩個多項式（以連結串列形式給出）相加的程式

假設我們有兩個多項式，我們需要求這兩個多項式的和。多項式需要用連結串列表示；多項式的項將用連結串列節點表示。每個連結串列節點將包含係數值、冪值以及指向下一個連結串列節點的指標。我們需要返回第三個連結串列，它是兩個連結串列多項式的和。

所以，如果輸入類似於

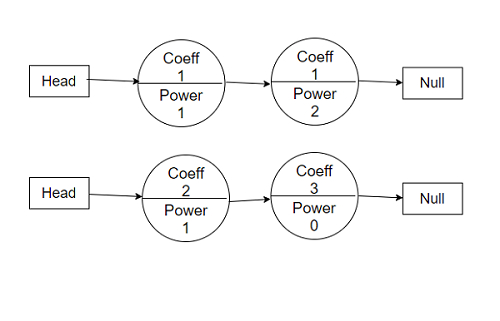
1x^1 + 1x^2 = 0 和 2x^1 + 3x^0 = 0，

那麼輸出將是 3x^1 + 1x^2 + 3x^0 = 0

為了解決這個問題，我們將遵循以下步驟 -

  • dummy := 一個新的多項式節點

  • node := 一個新的多項式節點

  • 當 poly1 和 poly2 不為空時，執行以下操作

    • 如果 poly1 的冪 > poly2 的冪，則

      • node 的下一個 := poly1

      • node := poly1

      • poly1 := poly1 的下一個

    • 否則，當 poly1 的冪 < poly2 的冪時，則

      • node 的下一個 := poly2

      • node := poly2

      • poly2 := poly2 的下一個

    • 否則，

      • coef := poly1 的係數 + poly2 的係數

      • 如果 coef 不為零，則

        • poly1 := poly1 的下一個

        • poly2 := poly2 的下一個

  • node 的下一個 := poly1 或 poly2

  • 返回 dummy 的下一個

讓我們看看下面的實現，以便更好地理解 -

示例

class polynomial:
def __init__(self, coeff = 0, pow = 0, nxt = None):
   self.coefficient = coeff
   self.power = pow
   self.next = nxt
def create_poly(expression):
   head = None
   for element in expression:
      if head == None:
         head = polynomial(element[0], element[1])
      else:
         temp = head
      while temp.next != None:
         temp = temp.next
         if temp.next == None:
            temp.next = polynomial(element[0], element[1])
            return head
def show_poly(head):
   temp = head
   while temp.next != None:
      print(str(temp.coefficient) + 'x^' + str(temp.power), end = ' + ')
      temp = temp.next
      if temp.next == None:
         print(str(temp.coefficient) + 'x^' + str(temp.power), end=' = 0')
def solve(poly1, poly2):
   dummy = node = polynomial()
   while poly1 and poly2:
      if poly1.power > poly2.power:
         node.next = node = poly1
         poly1 = poly1.next
      elif poly1.power < poly2.power:
         node.next = node = poly2
         poly2 = poly2.next
      else:
         coef = poly1.coefficient + poly2.coefficient
      if coef: node.next = node = polynomial(coef, poly1.power)
         poly1 = poly1.next
         poly2 = poly2.next
         node.next = poly1 or poly2
   return dummy.next
poly1 = create_poly([[1,1], [1,2]])
poly2 = create_poly([[2,1], [3, 0]])
poly3 = solve(poly1, poly2)
show_poly(poly3)

輸入

poly1 = create_poly([[1,1], [1,2]])
poly2 = create_poly([[2,1], [3, 0]])

輸出

3x^1 + 1x^2 + 3x^0 = 0

更新於: 2021年5月28日

3K+ 次檢視

開啟你的 職業生涯

透過完成課程獲得認證

開始學習
廣告