資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究使用 C++ 列印從根節點到指定節點路徑上的公共節點
在這個問題中，我們給定一棵二叉樹，並定義了二叉樹中的兩個節點。我們需要列印這兩個節點的公共祖先，即從根節點到這兩個節點的遍歷路徑中出現的公共節點。
二叉樹是一種特殊的樹，其每個節點最多有兩個子節點。因此，每個節點要麼是葉子節點，要麼有一個或兩個子節點。
例如，
祖先節點是指在樹中連線到較低級別節點的節點。
兩個節點的公共祖先節點是指在樹中是這兩個節點的祖先節點的節點。
例如 -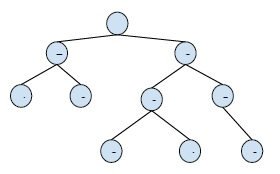 
在上面的二叉樹中，我們需要找到節點 0 和節點 6 的公共祖先。
輸出 - 3, 2
現在，基於這個問題，讓我們建立一個用於解決此問題的演算法：
演算法
Step 1 : Find the lowest common ancestor of the two nodes of the given tree. And print it. Step 2 : Traverse upward to the root node and print all the nodes that come in the path.
示例
現在，讓我們建立一個程式來演示此問題的解決方案：
#include <iostream>
using namespace std;
struct Node {
struct Node* left, *right;
int key;
};
Node* insertNode(int key){
Node* temp = new Node;
temp->key = key;
temp->left = temp->right = NULL;
return temp;
}
struct Node* LowestCommonAncestors(struct Node* root, int n1, int n2){
if (root == NULL)
return NULL;
if (root->key == n1 || root->key == n2)
return root;
Node* left_lca = LowestCommonAncestors(root->left, n1, n2);
Node* right_lca = LowestCommonAncestors(root->right, n1, n2);
if (left_lca && right_lca)
return root;
return (left_lca != NULL) ? left_lca : right_lca;
}
bool printAncestorNodes(struct Node* root, int target){
if (root == NULL)
return false;
if (root->key == target) {
cout << root->key << "\t";
return true;
}
if (printAncestorNodes(root->left, target) ||
printAncestorNodes(root->right, target)) {
cout << root->key << "\t”;
return true;
}
return false;
}
bool printcommonAncestors(struct Node* root, int first, int second){
struct Node* LCA = LowestCommonAncestors(root, first, second);
if (LCA == NULL)
return false;
printAncestorNodes(root, LCA->key);
}
int main(){
Node* root = insertNode(24);
root->left = insertNode(8);
root->right = insertNode(69);
root->left->left = insertNode(12);
root->left->right = insertNode(41);
root->right->left = insertNode(50);
root->right->right = insertNode(3);
root->left->left->left = insertNode(22);
root->right->left->left = insertNode(10);
root->right->left->right = insertNode(6);
if (printcommonAncestors(root, 6, 3) == false)
cout << "No Common nodes";
return 0;
}輸出
69 24
更新於: 2020年1月3日
105 次瀏覽
廣告